机器学习笔记
线性回归
- 很多自然现象是线性关系
- 一个非线性关系在很小的范围内也可以用线性关系描述:切线
- 对高斯随机的关系线性模型可以表示所有的参数
- 计算简单,容易理解
单参数
输出由一个输入决定
符号
- $\bar{x}$:平均值
- $s_{x}^2=s_{xx}$:方差
- $s_{x}=\sqrt{s_{xx}}$:标准差
- $s_{xy}$:协方差
- RSS: $\epsilon$ 平方和,不除N。Residual Sum of Square,Sum of Squared Residuals(SSR),Sum of Squared Errors(SSE)。RSS是一个二次函数,凸函数只有一个最小值
- MSE: Mean Square Error,除N
- Normalized MSE:$\frac{MSE}{s_{y}^{2}}\in[0,1]$
凹凸是往下看,往下凸。凸函数convex,凹函数concave
\[RSS(\beta_{0}, \beta_{1})=\sum_{i=1}^{N}(y_i-\hat{y}_i)^2\]- MSE:Mean Square Error,$\frac{1}{N}RSS$
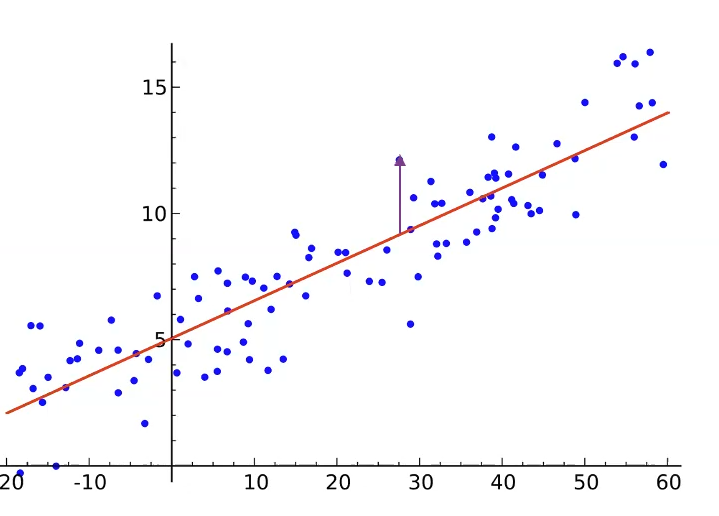
- Least Square Fit:最小化RSS,点和直线的垂直距离平方和最小
概率
PMF:Probability Mass Function \(PMF: P\{x=x_i\}=p_i\) 比如扔硬币,$P{x=0}=\frac{1}{2},P{x=1}=\frac{1}{2}$
\[\begin{aligned} E(x)&=\sum_{i=1}^N x_i*p_i \\ \delta^{2}_x=\operatorname{Var}(x)&=E(X-E(x))^{2} \\ &=\sum_{i=1}^{N}\left(x_{i}-E(x)\right)^{2} \cdot p_{i} \\ &=\sum_{i=1}^N\left[x_{i}^{2}-2 x_{i} E(x)+E(x)^{2}\right) P_{i} \\ &=\sum_{i=1}^N x_{i}^{2} P_{i}-2 E(x) \sum_{i=1}^N x_{i} P_{i}+E(x)^{2} \sum_{i=1}^N p_{i} \\ &=E\left(x^{2}\right)-2 E(x) \cdot E(x)+E(x)^{2} \\ & \Rightarrow E\left(x^{2}\right)-E(x)^{2}\\ E(x^2)&=Var(x)+E(x)^2\\ E(ax+by)&=aE(x)+bE(y) \end{aligned}\](TODO:推导)
样本的均值就是样本的期望,不带偏见的期望 \(\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i \\ E(\frac{1}{N}\sum_{i=1}^N x_i)=\frac{1}{N}\sum_{i=1}^N E(x_i)=E(x)\)
样本的方差约等于样本方差的期望,带偏见的期望。用了N个x计算均值和方差,方差的自由度不再是N而是N-1
(TODO:推导)
\[s_{xx}=\frac{1}{N}\sum_{i=1}^N (x_i-\bar{x})^2 \\ E(\sum_{i=1}^N (x_i-\bar{x})^2) = (N-1)\delta_x^2 \\ E(s_{xx})=\frac{N-1}{N}\delta_x^2\]不带偏见的方差,Bessel’s Correction \(s_{xx}=\frac{1}{N-1}\sum_{i=1}^N (x_i-\bar{x})^2 \\\)
算 $\beta$
均值 \(\bar{x} = \frac{1}{N}\sum_{i=1}^{N}x_{i} \\ \bar{y} = \frac{1}{N}\sum_{i=1}^{N}y_{i} \\\)
xy协方差 covariance \(s_{xy}=\frac{1}{N}\sum_{i=1}^{N}[(x_{i}-\bar{x})*(y_{i}-\bar{y})]\)
xy协方差是 $(x-\bar{x})$ 和 $(y-\bar{y})$ 两个向量的内积
x方差 variance \(\begin{align} s_{xx} &= s_{x}^2=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\bar{x})^{2} \\ s_{x} &= \sqrt{s_{xx}} \end{align}\)
y方差 \(\begin{align} s_{yy} &= s_{y}^2=\frac{1}{N}\sum_{i=1}^{N}(y_{i}-\bar{y})^{2} \\ s_{y} &= \sqrt{s_{yy}} \end{align}\)
方差 = 平方和平均值 - 平均值的平方 \(\begin{align} s_{xx}&=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\bar{x})^2\\ &=\frac{1}{N}\sum_{i=1}^{N}(x_{i}^2-2x_{i}\bar{x}+\bar{x}^2)\\ &=\frac{1}{N}\sum_{i=1}^{N} x_{i}^2 -2\bar{x}\frac{1}{N}\sum_{i=1}^{N}{x_{i}} + \bar{x}^2\\ &=\frac{1}{N}\sum_{i=1}^{N} x_{i}^2 - \bar{x}^2 \end{align}\)
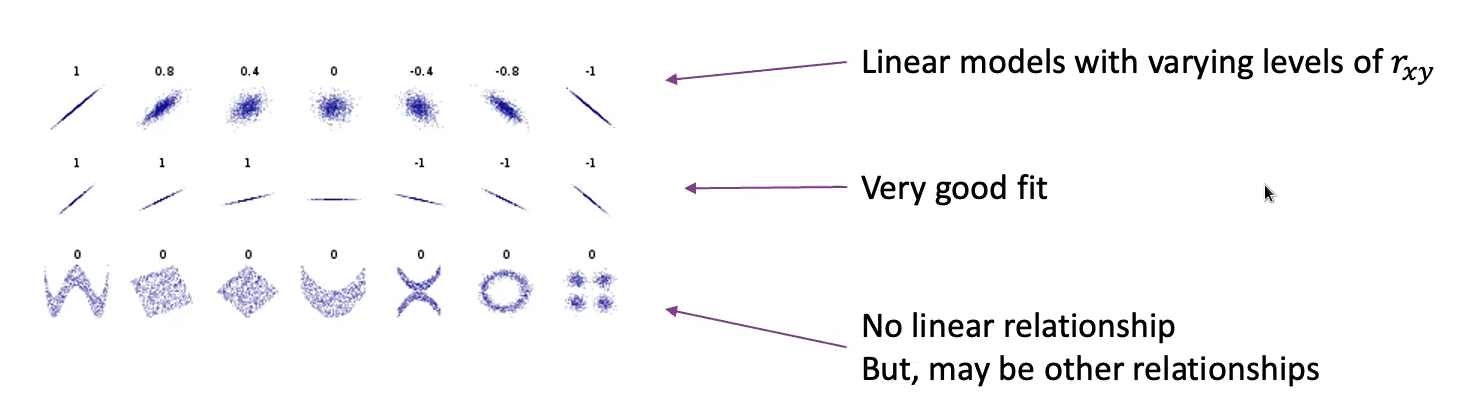
- x和y的关联系数 \(r_{xy}=\frac{s_{xy}}{s_{x}s_{y}} \in [-1, 1]\)
$s_x, s_y$ 是 $(x-\bar{x}),(y-\bar{y})$ 的长度
根据柯西不等式
| $s_{xy} = | (x-\bar{x}) | * | (y-\bar{y}) | *cos(x-\bar{x},y-\bar{y}) \le s_{x}\cdot s_{y}$ |
$r_{xy}^2$ 越接近1,x和y的关系越接近线性
- 平方误差 \(RSS(\beta_{0}, \beta{1})=\sum_{i=1}^{N} (y_{i}-\beta_{0}-\beta_{1}x_{i})^2\)
二次函数是凸函数,所以导数为0的点RSS最小
\(\begin{align} \frac{\partial RSS(\beta_{0}, \beta_{1})}{\partial \beta_{0}}&=\sum_{i=1}^{N}2*(y_{i}-\beta_{0}-\beta_{1}x_{i})*-1 \\ &=-2*\sum_{i=1}^{N}\epsilon_{i}\\ \Rightarrow \sum_{i=1}^{N}\epsilon_{i}&=0 \end{align}\) 一组好的 $\beta$ 应该让线在所有点中间,往上和往下的误差相等
\(\begin{align} \frac{\partial RSS(\beta_{0}, \beta_{1})}{\partial \beta_{1}} &= \sum_{i=1}^{N}2*(y_{i}-\beta_{0}-\beta_{1}x_{i})*(-x_{i}) \\ &=-2*\sum_{i=1}^{N}\epsilon_{i}*x_{i}&\\ \Rightarrow \sum_{i=1}^{N}\epsilon_{i}*x_{i}&=0 \\ \end{align}\) $\epsilon$ 和x的内积=0,说明误差应该和数据垂直
\(\begin{align} &\sum_{i=1}^{N}\epsilon_{i}=0\\ \Rightarrow & \sum_{i=1}^N(y_i-\beta_0-\beta_1x_i)=0 \\ \Rightarrow & \sum_{i=1}^N y_i-N\beta_0-\beta_1\sum_{i=1}^N x_i =0\\ \Rightarrow & N\bar{y}-N\beta_0-N\beta_1\bar{x} =0 \\ \Rightarrow & \bar{y}=\beta_0+\beta_1\bar{x} \end{align}\) 模型的直线应该过均值点
\[\begin{align} &\sum_{i=1}^{N}x_i\epsilon_i=0\\ \Rightarrow & \sum_{i=1}^N x_i(y_i-\beta_0-\beta_1x_i)=0 \\ \Rightarrow & \sum_{i=1}^N x_iy_i - x_i\beta_0 -\beta_1x_i^2 = 0\\ \Rightarrow & \sum_{i=1}^N y_i-\beta_0-\beta_1x_i = 0 \\ \Rightarrow & \sum_{i=1}^N y_i - \bar{y} + \beta_1\bar{x}-\beta_1x_i=0 \\ \Rightarrow & \sum_{i=1}^N y_i - \bar{y} = \beta_1\sum_{i=1}^N x_i-\bar{x} \\ \Rightarrow & \beta_1 = \sum_{i=1}^N \frac{y_i - \bar{y}}{x_i-\bar{x}} \\ \Rightarrow & \beta_1 = \sum_{i=1}^N \frac{(y_i - \bar{y})*(x_i-\bar{x})}{(x_i-\bar{x})*(x_i-\bar{x})} \\ \Rightarrow & \beta_1 = \frac{s_{xy}}{s_{xx}} = \frac{r_{xy}s_{y}}{s_{x}}\\ \end{align}\]$\frac{s_y}{s_x}$ 模型横向走过x的一个标准差,纵向走过y的一个标准差。模型的y和x越相关,斜率越大。
\[\begin{aligned} \beta_1 &= \frac{s_{xy}}{s_{xx}}=\frac{r_{xy}s_{y}}{s_{x}} \\ \quad \beta_0 &= \bar{y} - \beta_1\bar{x} \end{aligned}\]\(\begin{aligned} min RSS(\beta_{0}, \beta_{1})&=\sum_{i=1}^N\epsilon_i^2\\ &=\sum_{i=1}^N \epsilon_i(y_i-\beta_0-\beta_1x_i)\\ &=\sum_{i=1}^N\epsilon_iy_i - \sum_{i=1}^N \epsilon_i\beta_0 - \sum_{i=1}^N \epsilon_i\beta_1x_i\\ &=\sum_{i=1}^N\epsilon_iy_i - \beta_0\sum_{i=1}^N \epsilon_i - \beta_1\sum_{i=1}^N \epsilon_ix_i\\ &=\sum_{i=1}^N\epsilon_iy_i \\ &=\sum_{i=1}^N (y_i-\beta_0-\beta_1x_i)y_i\\ &=\sum_{i=1}^N y_i^2- \sum_{i=1}^N\beta_0y_i - \sum_{i=1}^N\beta_1x_iy_i\\ &=N(\bar{y^2} - \beta_0\bar{y}-\beta_1\bar{xy}) \\ &=N(\bar{y^2} - (\bar{y} - \beta_1\bar{x})\bar{y}-\beta_1\bar{xy}) \\ &=N(\bar{y^2} - \bar{y}^2 + \beta_1\bar{x}\bar{y}-\beta_1\bar{xy}) \\ &=N(s_{yy} - \beta_1s_{xy}) \\ &=N(s_{yy} - \frac{s_{xy}}{s_{xx}}s_{xy}) \\ &=Ns_{yy}(1 - \frac{s_{xy}^2}{s_{xx}s_{yy}}) \\ &=Ns_{yy}(1-r_{xy}^2) \end{aligned}\) x,y非常相关的时候误差小;y越平越小。最终的误差跟怎么取x没有关系
多参数
多个输入决定输出
符号
- $x_i=(x_{i,1}, x_{i,2}, … , x_{i,k})$
- $\hat{y}i=\beta{0} + \beta_{1}x_{i,1} + … + \beta_{k}x_{i,k}$
$A^{T}A$ 是A的方差,对 $s_{xx}$;$A^{T}Y$ 是A和Y的关联,对 $s_{xy}$
(TODO:jabobian matrix) (TODO:推导beta和minRss)