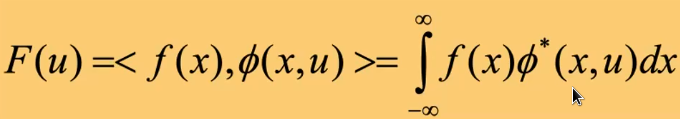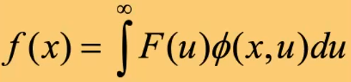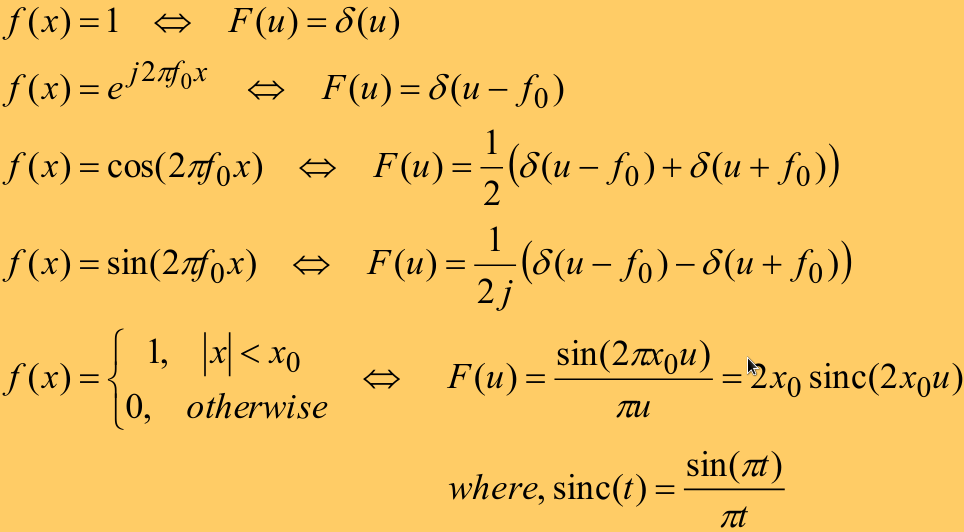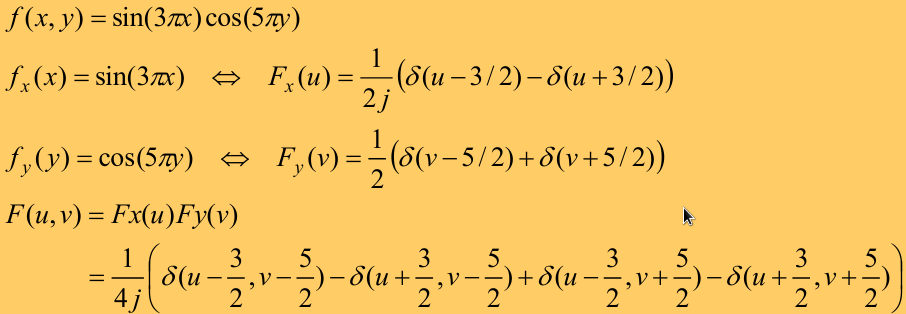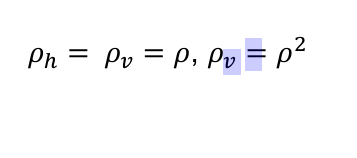图像处理笔记
- Rod:视杆,亮度,120M
- Cone:视椎,颜色,6M
(TODO:怎么判断三元色选的好不好)
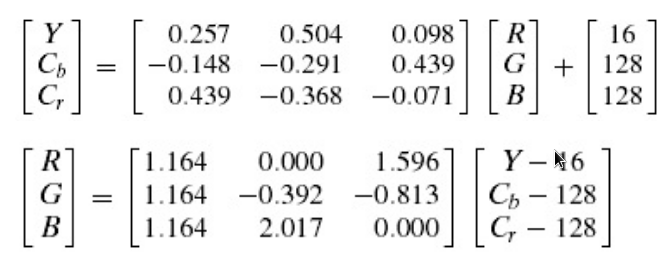
颜色表示
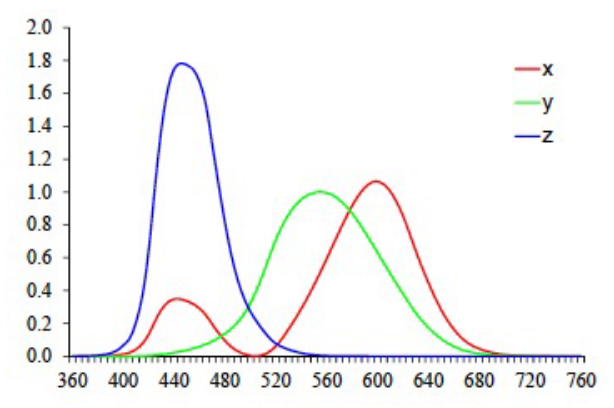
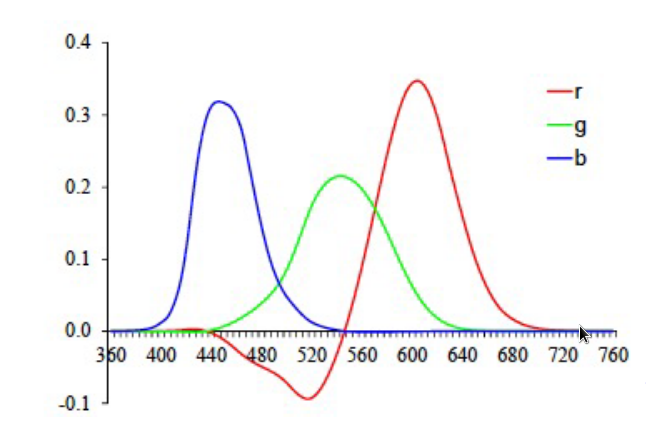
- 三元色:Trichromatic color mixing
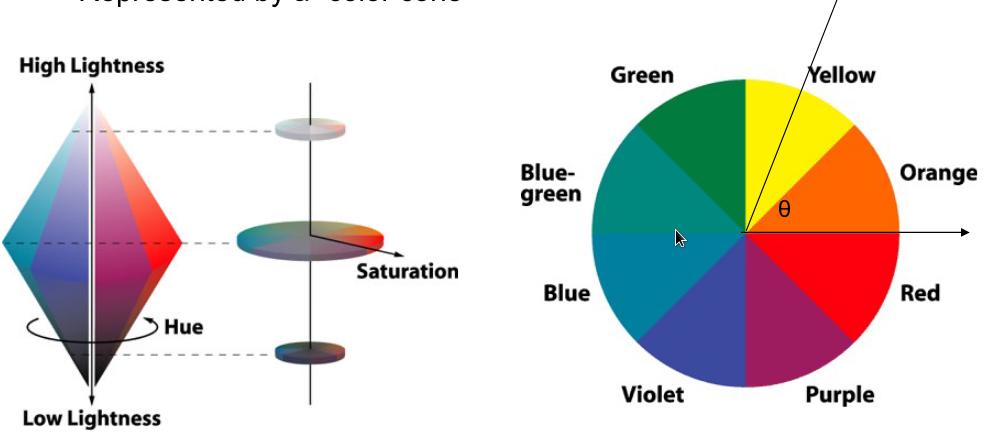
- 亮度+颜色
颜色范围
- SDR:Standard Dynamic Range,8 bit
HDR:High dynamic range,16 bit
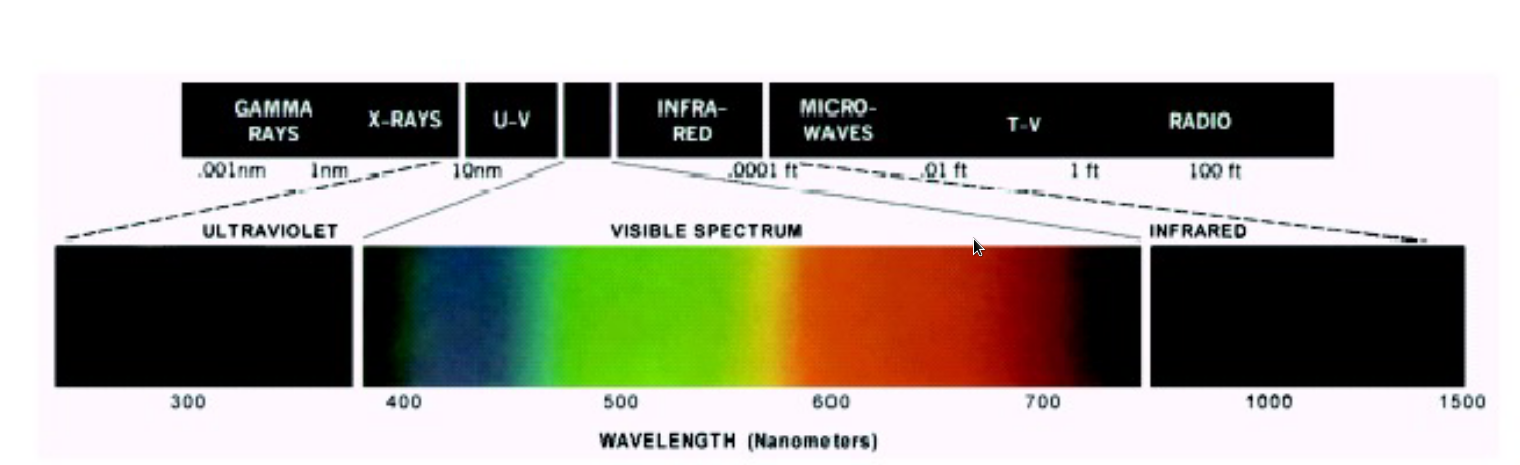
- Illuminating source
- 发光频率决定颜色
- R+G+B=White
- 一般用RGB
- Reflecting source
- 颜色=照射频率-吸收频率
- R+B+G=Black
- 一般用CMY
- CMYK:Cyan(青), Magenta(洋红), Yellow(黄), Black(黑)
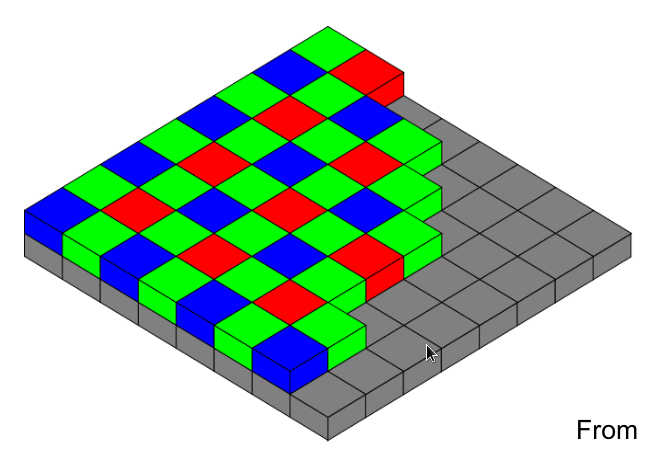
传感器上RGB交替
颜色校准:白色的RGB要相等
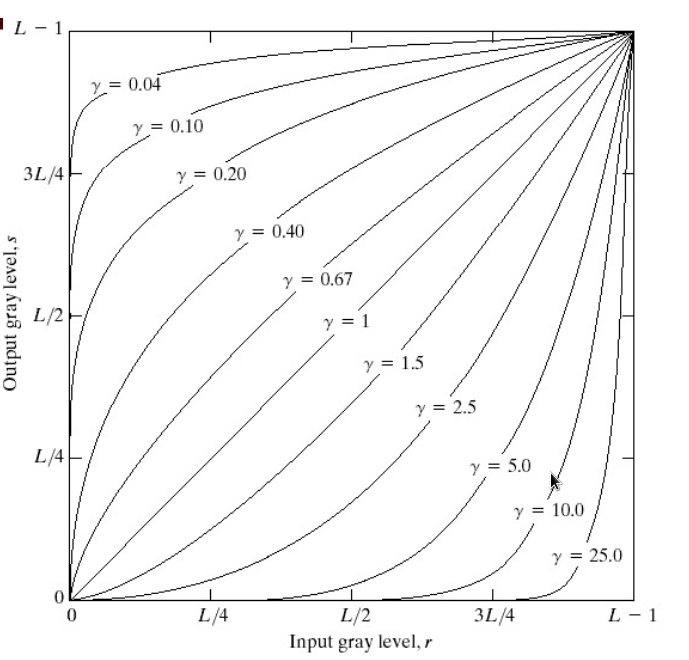
Gamma Correction:显示的强度和真实的强度是非线性的
(TODO:)
视频
- Standard Definition:720x480,4:2,25-30fps,隔行或逐行扫描,8 bit
- High Definition,1080p,2K:1920x1080,16:9/2:1,最高60fps
- Ultra High Definition,4K:3840x2160,16:9,最高120fps,16 bit,发行10~12bit,色域更广
对比度
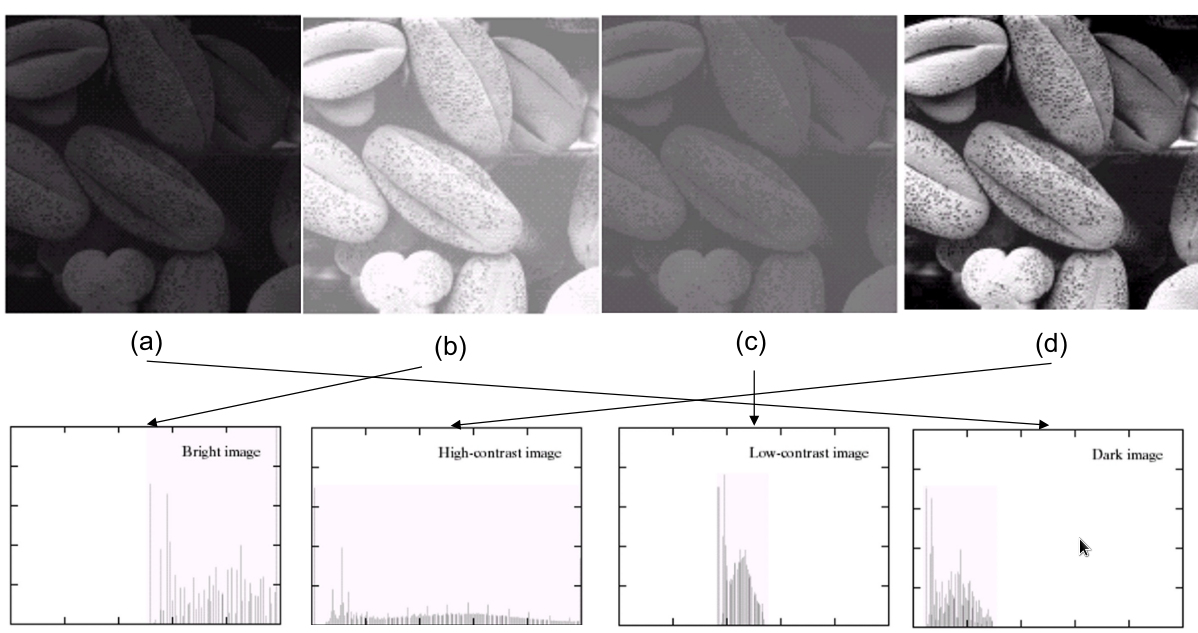
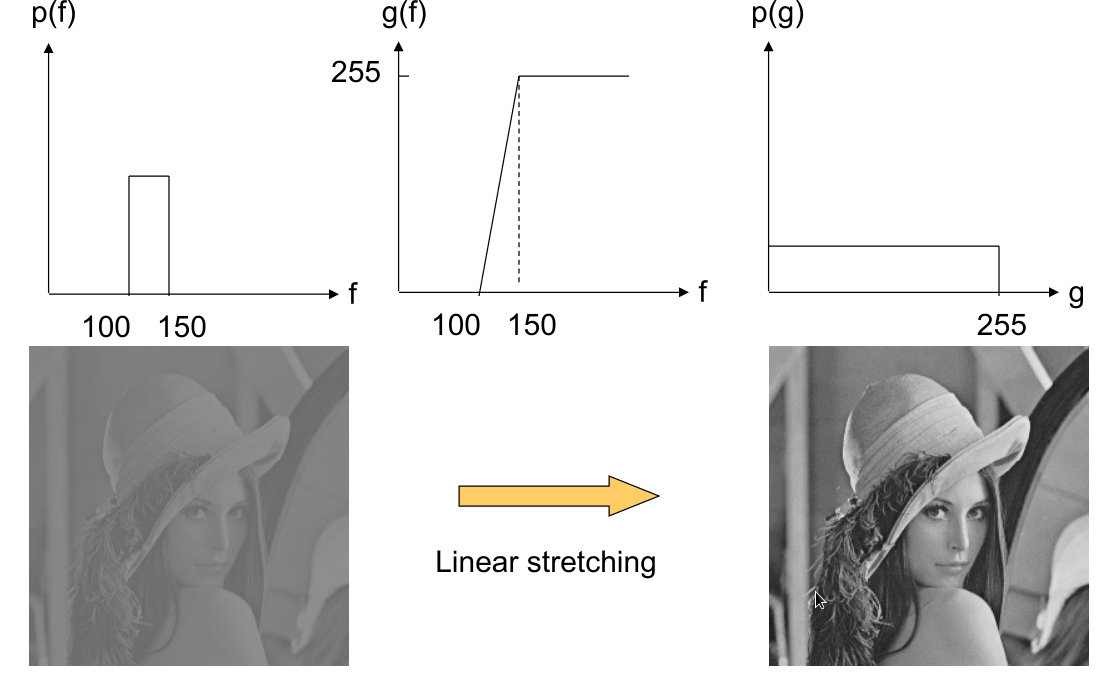
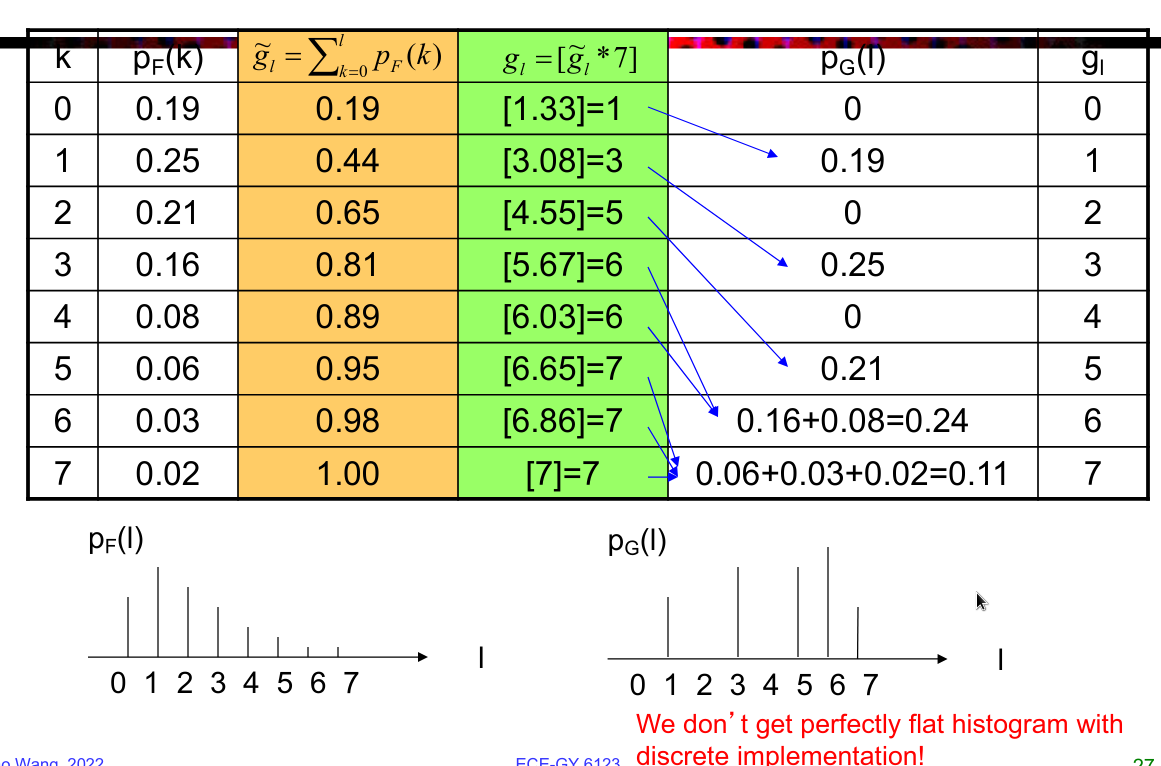
低对比度的图像看起来颜色非常贴近,理想图像颜色在直方图里分布宽且均匀
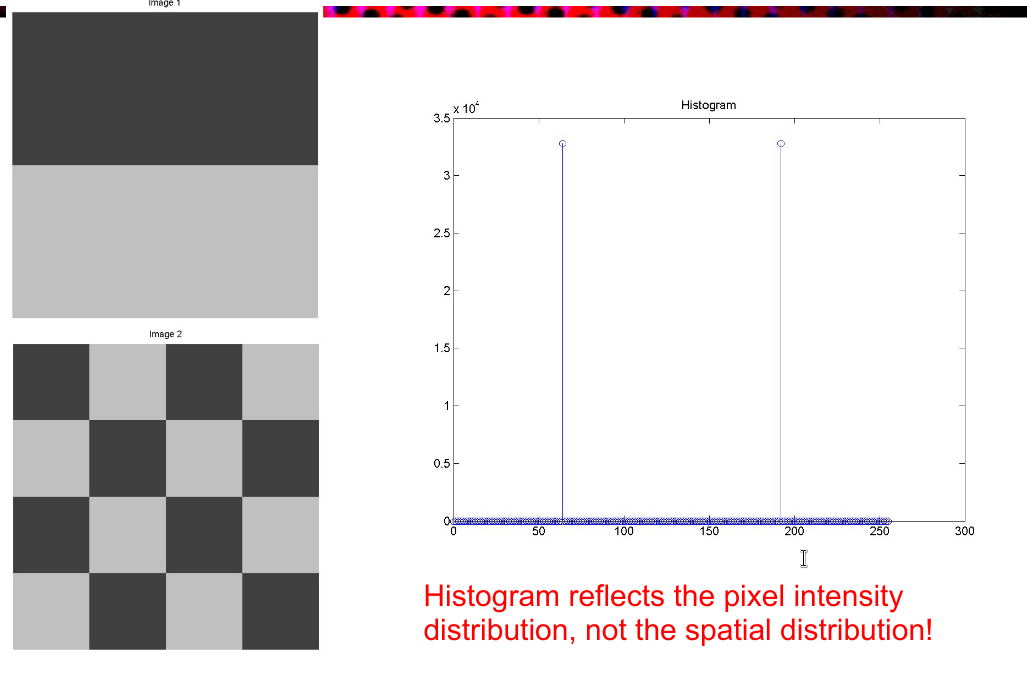
直方图只能总结图像强度分布,很不一样的图片也可以有一样的直方图
增强对比度
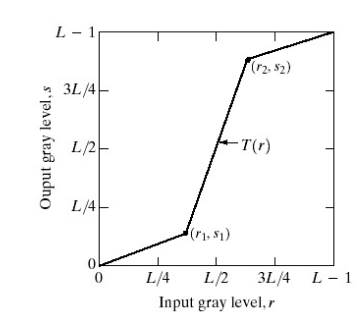
逐个像素改变强度值,函数非递减
- 固定函数
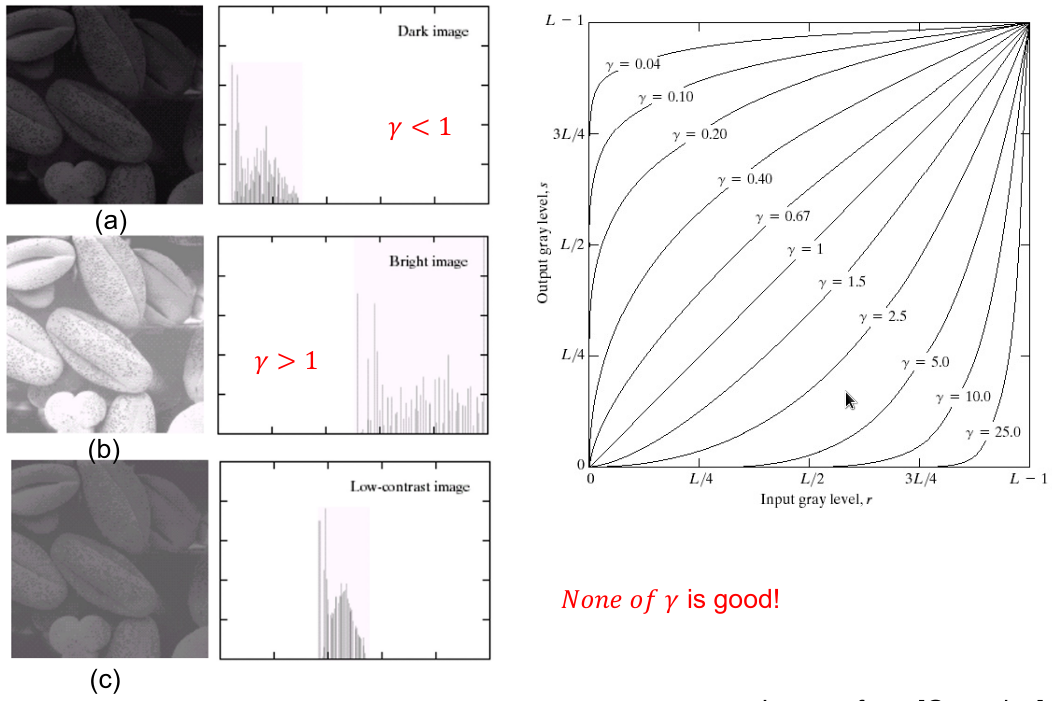
(TODO:图片power law)
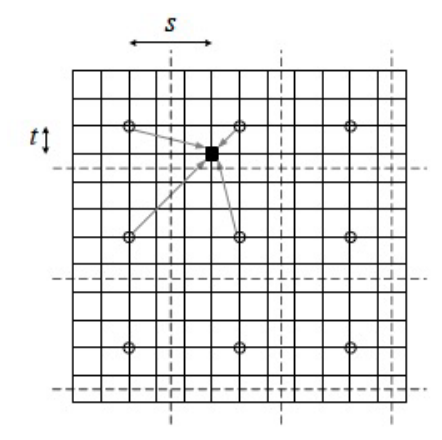
局部增强:图像整体强度分布平均,但是局部不平均,可以滑动窗口针对局部增强对比度
在一些不重叠的区域里计算变换函数
傅立叶变换
f(m,n)
可分:函数可以表示为两个函数积 $f(m,n)=f_v(m)f_h(n)$,2D矩阵可以表示为两个1D矩阵积(没一行都成比例,每一列都成比例)
函数内积,投影:一个函数乘另一个函数的共扼在整个定义域上积分
$\phi(x,idx)$ 第idx个基底。
orthonormal:单位,垂直 \(\int_{-\infty}^\infty \phi(x, u_1)\phi^*(x,u_2)dx=\{ \begin{matrix} 1, \quad u_1=u_2 \\ 0, \quad u_1\ne u_2 \end{matrix}\)
用的是 $2\pi u$ 而不是 $\omega$ ,所以没有 $\frac{1}{2\pi}$
时域宽,低频信号多,频域窄。时域越宽越接近常数的频率0,频域越接近冲击。频域零点在1/时域方波长度(连续是1/2时域零点,离散是1/N,离散从0开始) 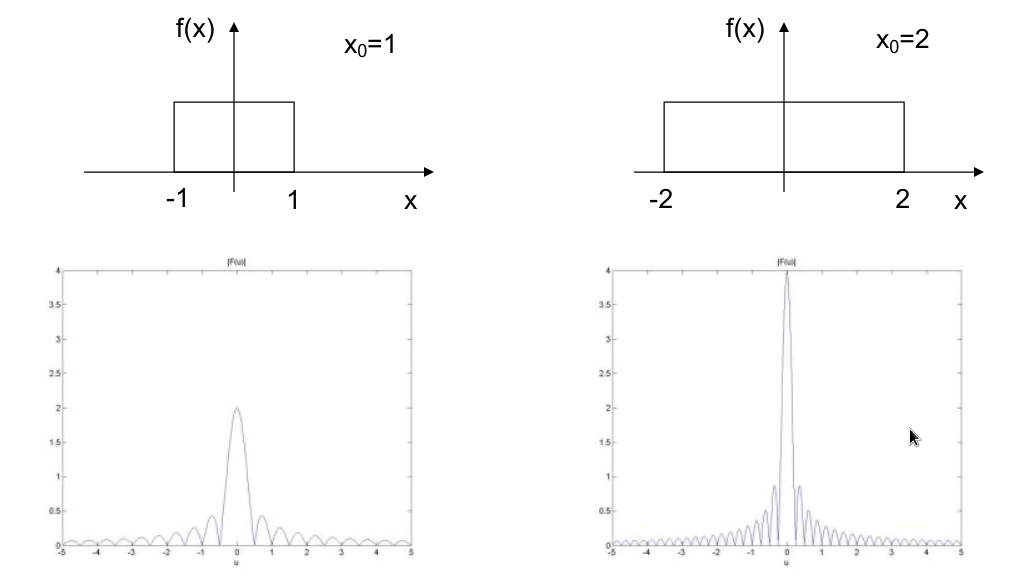
时域是实函数,频域性质
2D傅立叶
1D单位正交基底相乘得到的2D基底还是单位正交的
- 两个垂直方向的频率:比如x和y方向上单位长度(整幅图)分别 $f_x, f_y$ 周期
- 频率和角度:角度是频率最高的方向 $atan(\frac{y}{x})$,这个方向上的频率 $f_m$ 是 $\sqrt{f_x^2+f_y^2}$
$F{f(x)}=\frac{1}{2j}(\delta(u-f_x,v-f_y)-\delta(u+f_x, v+f_y))$ 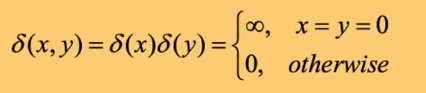
可分2D傅立叶:如果f(x, y)可以表示为g(x)*h(y)的形式,用g(x)傅立叶得F(u),用h(y)傅立叶得F(v),F(u, v)=F(u)乘F(v)
2D傅立叶旋转:空间可频域一起转
DSFT, DFT
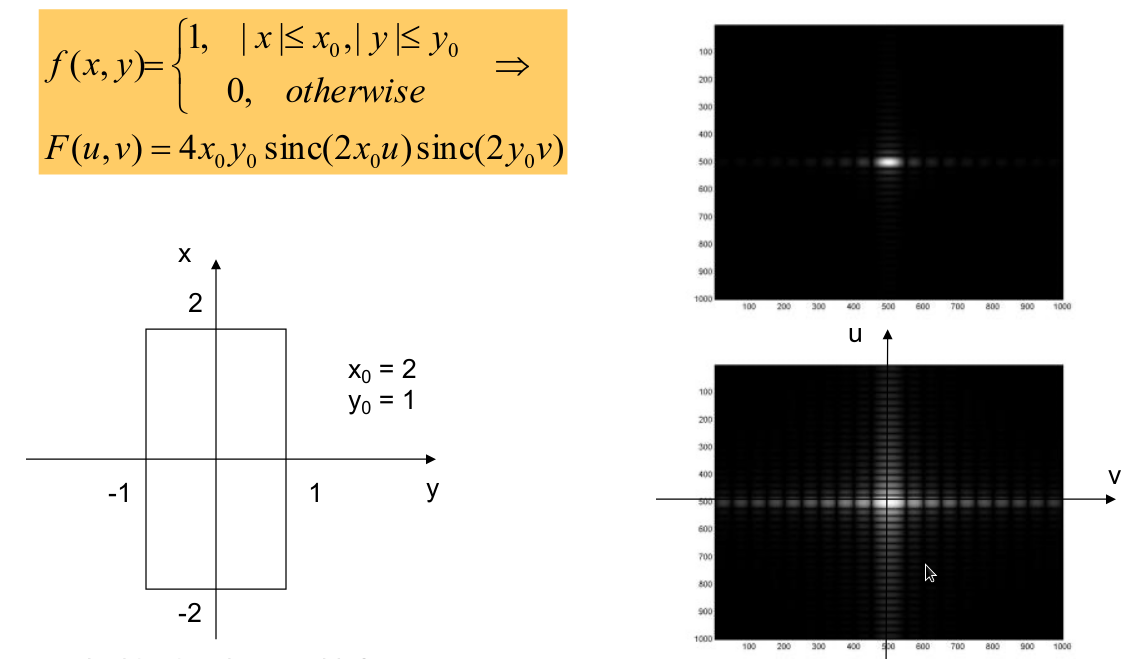
空间内直线在dft里垂直方向会有一条亮线,用所有的频率做一条直线出来
有周期的会有亮点;亮线和图像线垂直;很规整的sinc,比较发散
卷积
2D卷积两个坐标轴翻转,到第三象限
滤波器:h(m,n) 一个系统的冲击反馈(point spread function)
point spread function:一个点的输入一般result in一个区域,point spread越小分辨率越高
- 图像M*N,filter K*L,输出 M+N-1, K+L-1
- 图像M*N,filter (2k+1, 2k+1),蓝色和橙色区域取决于padding
可分滤波器可以在x,y上单独做
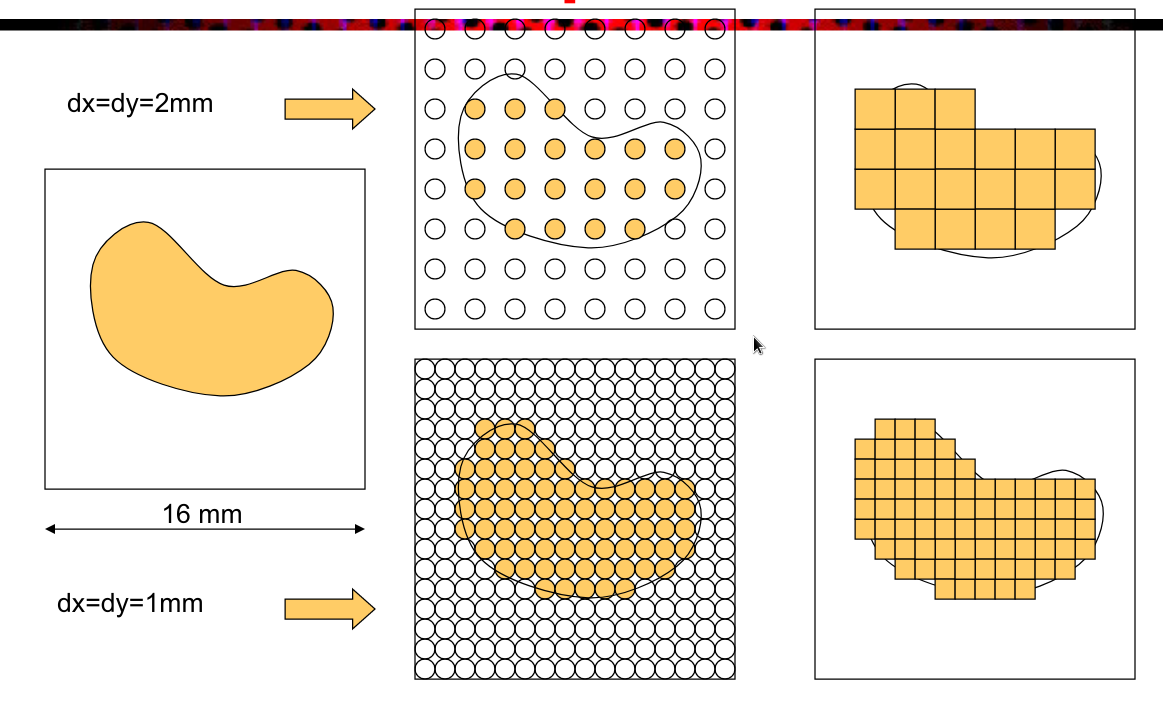
采样&插值
- 采样:连续到离散
- 插值:离散到连续
符号
- 采样间隔:$\Delta_x$,$\Delta_y$
- 采样频率:$f_{s,x}=\frac{1}{\Delta_x}$,$f_{s,y}=\frac{1}{\Delta_y}$,时间维度的采样率fps
- nyquist频率:$f_{m,x}$,$f_{m,x}$,采样频率的一半
- 连续图像:$f(x, y)$
- 采样图像:$f_s(m, n)$
重建图像:$\hat{f}(x, y)$
- 采样
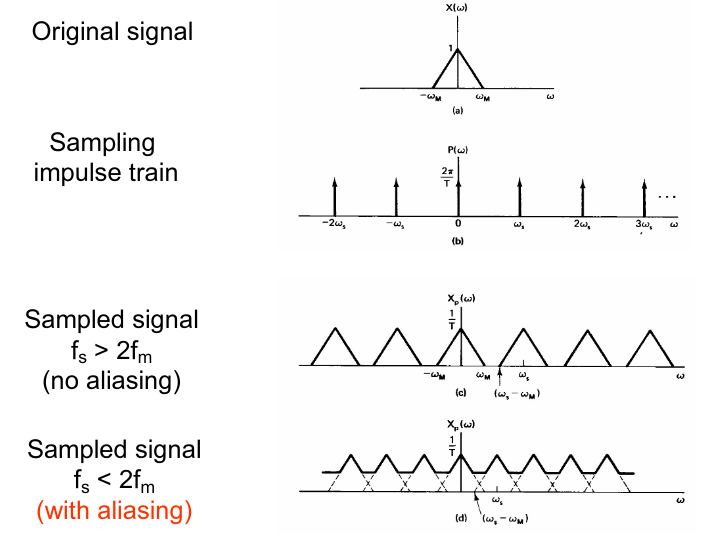
- 采样频率大于1/2信号最大频率
- 时域乘脉冲序列,间隔 $1/\Delta$,幅度1
- 频域卷脉冲序列,间隔 $\Delta$,幅度 $\frac{1}{\Delta_x\Delta_y}$
- 脉冲序列傅立叶还是脉冲序列
- 通过加频域的多个信号返回时域信号,频域信号的幅度小
- 重建
- 频域乘低通,截止频率 = 1/2采样频率,幅度 $\Delta_x\Delta_y$
- 时域和sinc卷积
- 把sinc放在每一个像素上,幅度是像素强度,最后求和
- 采样图像里m,n对重建图像x,y的贡献权重是2d sinc在x,y和m,n距离位置的取值
采样:采样结果M行N列 \(f_s(m, n)=f(m\Delta_x, n\Delta_y) \quad m=0,1,...,M, \quad n=0,1,...,N \\\)
脉冲序列: \(\begin{aligned} p(x, y)&=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} \delta\left(x-m \Delta_{x}, y-n \Delta_{y}\right)\\ \end{aligned}\)
脉冲序列的傅立叶:
- 1D:采样结果长度为N
频率是 $f_s$,所以频率是 $f_s$ 整数倍的都过采样点
- 2D
- 采样时域:信号 $\times$ 脉冲序列 \(\begin{aligned} \tilde{f_{s}}(x, y)&=f(x, y) \times p(x, y)\\ &=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f\left(m \Delta_{x}, n \Delta_{y}\right) \delta\left(x-m \Delta_{x}, y-n \Delta_{y}\right) \\ &=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_{s}(m, n) \delta\left(x-m \Delta_{x}, y-n \Delta_{y}\right) \\ \end{aligned}\)
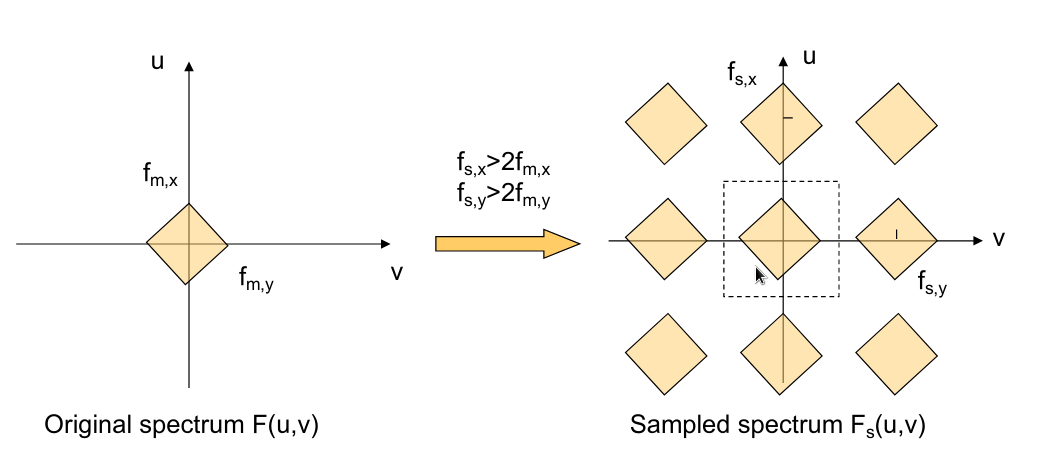
采样频域:信号 * impulse train \(\begin{aligned} F_{s}(u, v)&=F(u, v) * P(u, v) \\ P(u, v)&=\frac{1}{\Delta x \Delta y} \sum_{m, n} \delta\left(u-m f_{s, x}, v-n f_{s, y}\right) \\ \Rightarrow F_{s}(u, v)&=\frac{1}{\Delta x \Delta y} \sum_{m, n} F\left(u-m f_{s, x}, v-n f_{s, y}\right) \\ &\text { where } f_{s, x}=\frac{1}{\Delta x}, f_{s, y}=\frac{1}{\Delta y}\\ \end{aligned}\) 这里如果采样频率不大于固有频率的二倍,频域信号就会有重合,就会有伪影
- 重建时域:采样信号 * 2d sinc $$ \begin{aligned} H(u, v)&=\left{\begin{array}{cc} \Delta x \Delta y & |u| \leq \frac{f_{s, x}}{2},|v| \leq \frac{f_{s, y}}{2}
& 0 \quad \text { otherwise } \end{array} \Leftrightarrow h(x, y)=\frac{\sin \pi f_{s, x} x}{\pi f_{s, x} x} \cdot \frac{\sin \pi f_{s, y} y}{\pi f_{s, y} y}\right.\
\hat{f}(x, y)&=\tilde{f}{s}(x, y) * h(x, y)
&=\sum{m=0}^{M-1} \sum_{n=0}^{N-1} f_{s}(m, n) \delta\left(x-m \Delta_{x}, y-n \Delta_{y}\right) * h(x, y)
&=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_{s}(m, n) h\left(x-m \Delta_{x}, y-n \Delta_{y}\right)
h(x, y)&=\frac{\sin \left(\pi f_{s, x} x\right)}{\pi f_{s, x} x} \frac{\sin \left(\pi f_{s, y} y\right)}{\pi f_{s, y} y}
\hat{f}(x, y)&=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_{s}(m, n) \frac{\sin \pi f_{s, x}(x-m \Delta x)}{\pi f_{s, x}(x-m \Delta x)} \frac{\sin \pi f_{s, y}(y-m \Delta y)}{\pi f_{s, y}(y-m \Delta y)} \end{aligned} $$
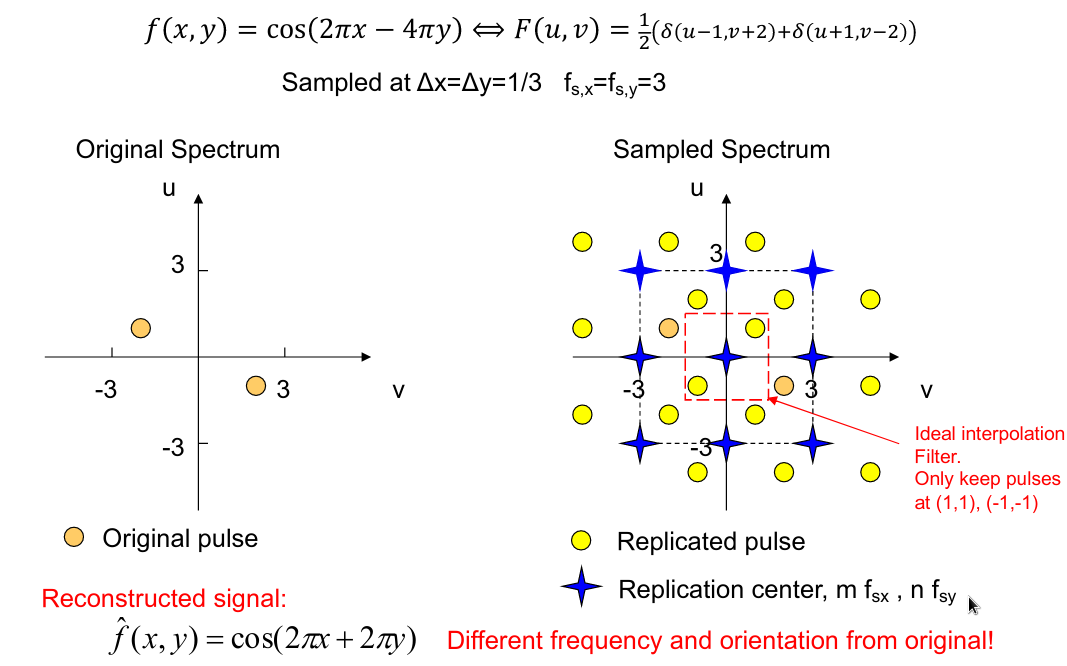
$采样率低\to空间间隔大\to频域间隔小\to和冲击卷完有叠加\to采样完图像里能看到比原图周期低的信号\to伪影\to重建信号比原信号频率低$
采样的频率应该大于信号固有频率的2倍,一个周期至少2个点
x采样率够,y采样率不够
jaggie
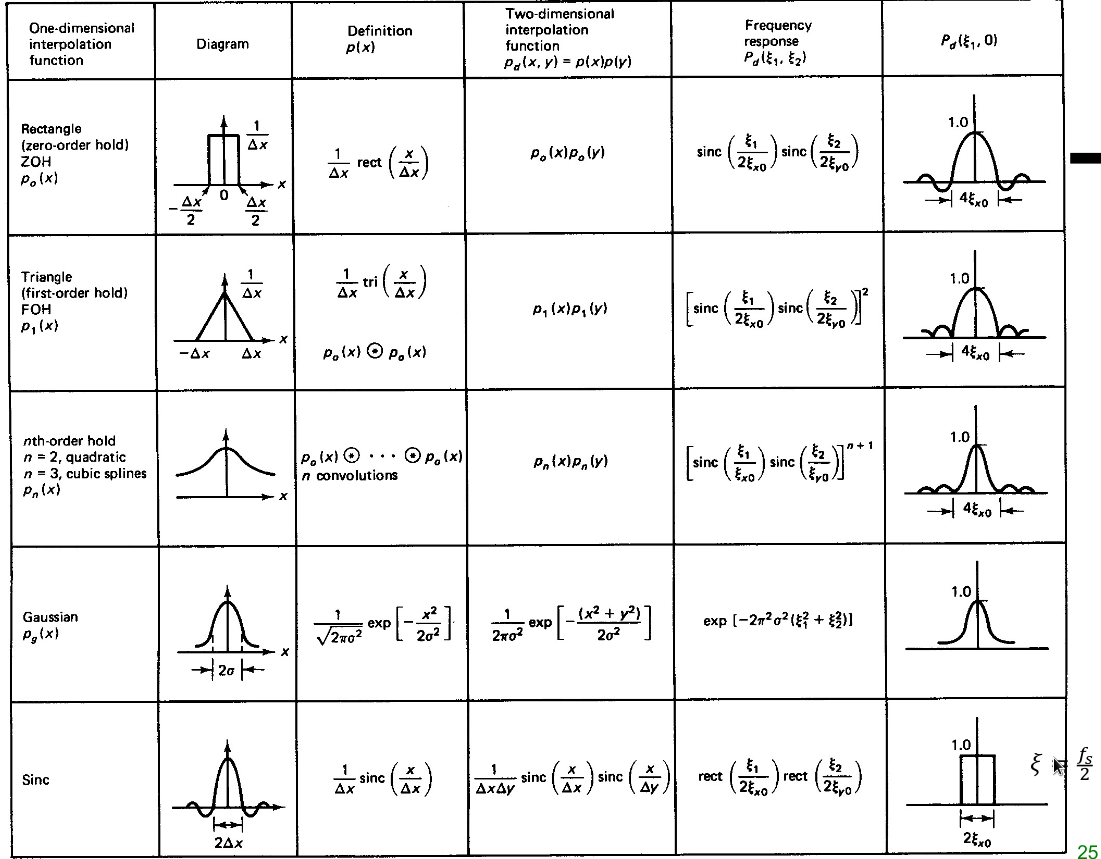
插值滤波不可能是理想低通,那样空间域无限大。Nyquist filter 性质:
- 低通:超过采样频率一半的信号都是重复的
- 递减:离一个点越远,对这个点插值的贡献应该越小
- 偶函数
- 可分: $h(x,y)=h_v(x) \cdot h_h(y)$,减少计算
- $h(0,0)=1$, $h(m\Delta_x, n\Delta_y)=0$:采样值原样进入重建图像
prefilter,sampling filter:实际图像里可能包含非常高频的信号,在采样之前先过一个截止频率 $f_c=\frac{f_s}{2}$ 的滤波器。不做prefilter可以保留更多细节,但是会有低频的纹理
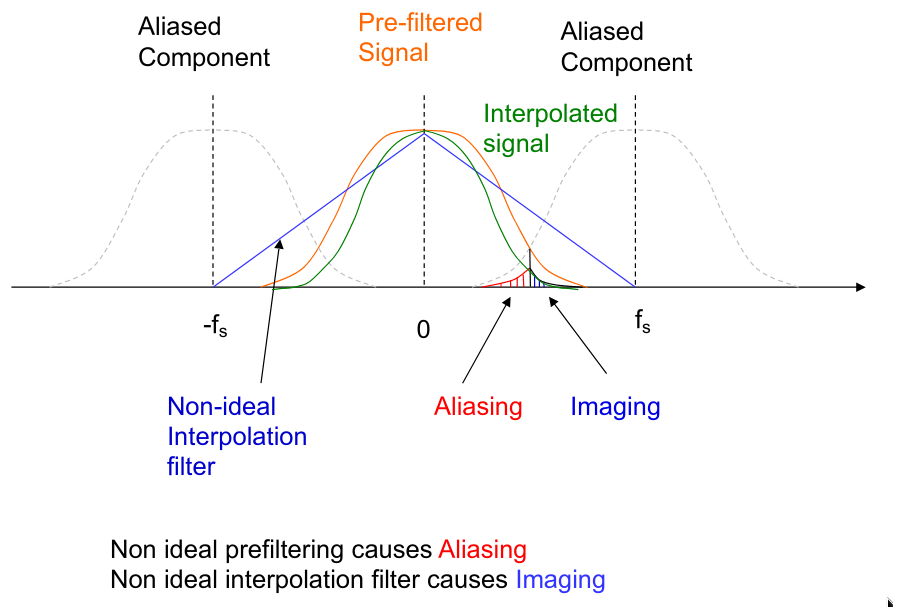
- aliasing:采样前滤波带来的问题。原信号经过prefilter还是有高频信号,带来比1/2采样频率低的噪声。体现在直的线变阶梯,条纹有比原来频率低的。
- imaging:插值的滤波器带来的问题。不是理想低通,截止频率之外还是有信号,带来比1/2采样频率高的噪声
相机
- 相邻两个同颜色传感器中心的距离是采样间隔
- 传感器的输出是一个面积上的光强总数,相当于采样前滤波去掉高频信号
aliasing 例子 https://www.red.com/red-101/cinema-temporal-aliasing
观察的时候眼睛和脑子做插值的低通滤波
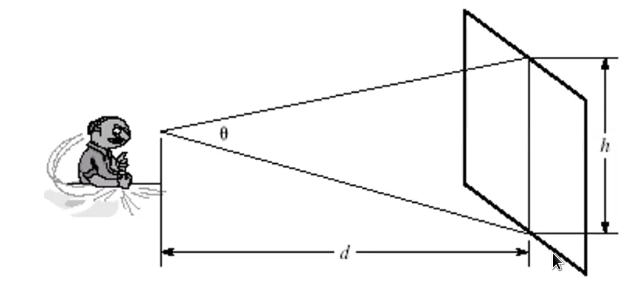
角频率:看的时候重要的是单位角度的频率
- 屏幕越远频率越高
- 屏幕越大频率越低
- 时间上通常能看到60hz,实际可以更快因为眼睛会跟着物体动,相对频率变小。显示60hz的信号需要120hz的采样率。
- 空间上通常能看到30 cycle per degree,空间上应该捕捉到60 cycle per degree
- 时间上频率越高,空间上同样角频率的信号越不敏感。时间快的场景分辨率就可以低
- 亮度越高,能分辨的帧率越高
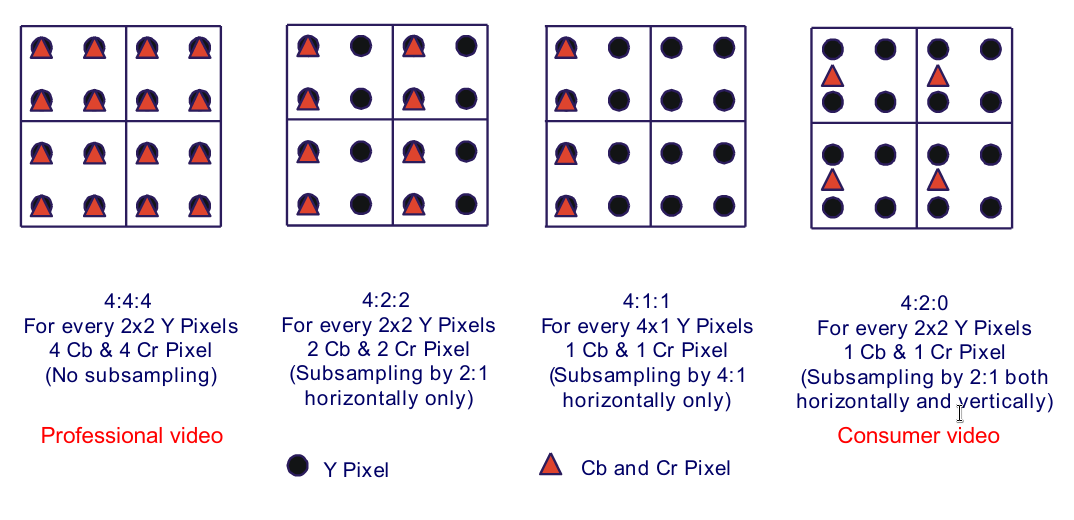
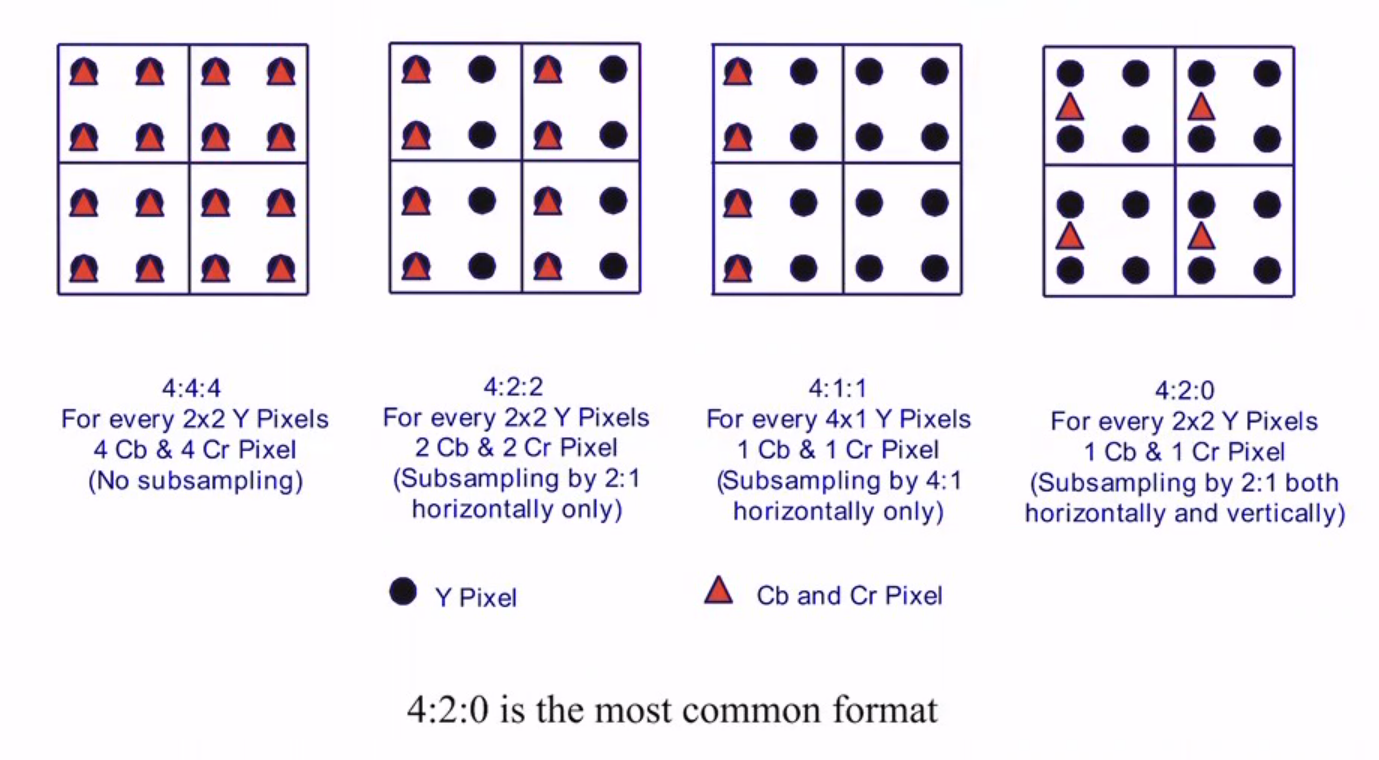
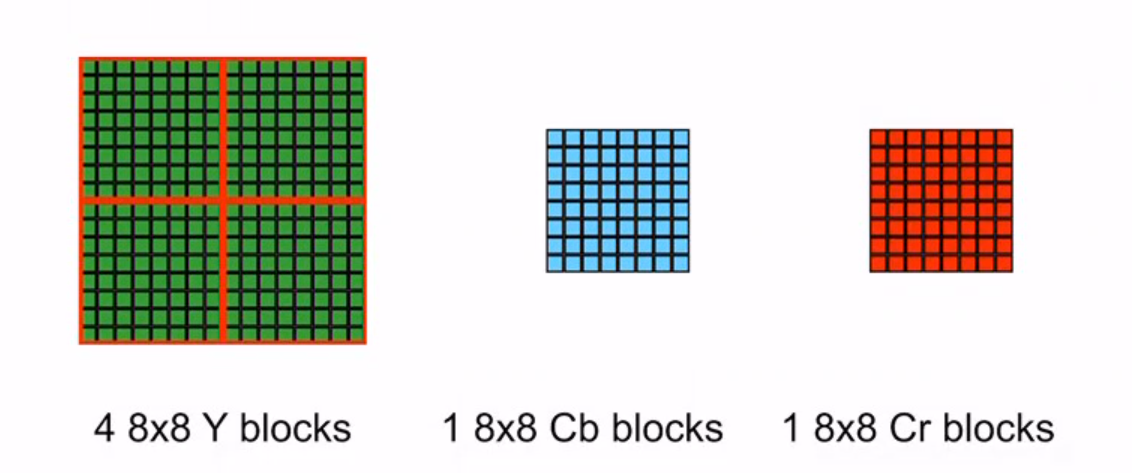
眼睛对亮度更敏感,4个Y不需要4个cbcr
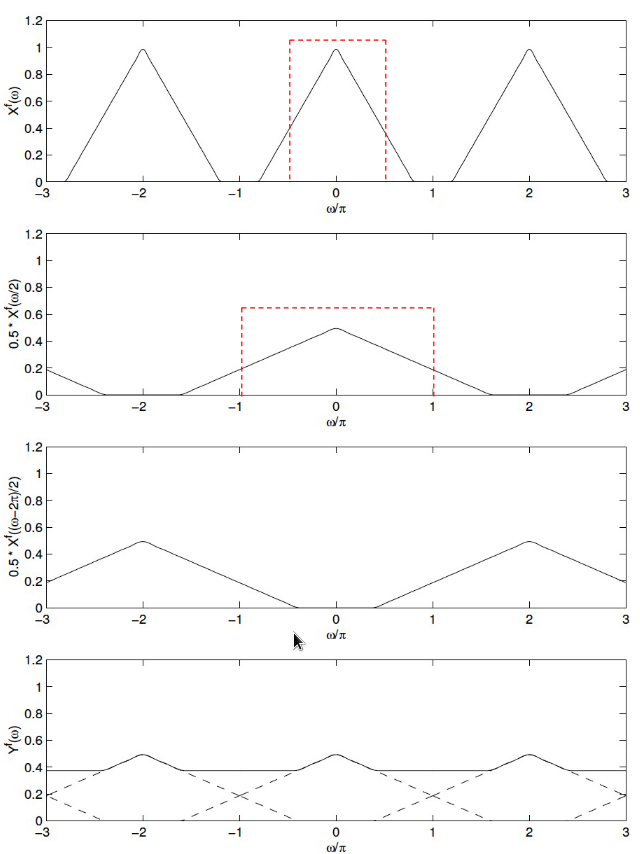
下采样周期变短,频率变高,可能会alias,下采样前先过一个half band filter,cutoff频率应该是固有频率1/4
upsample:填0,卷积 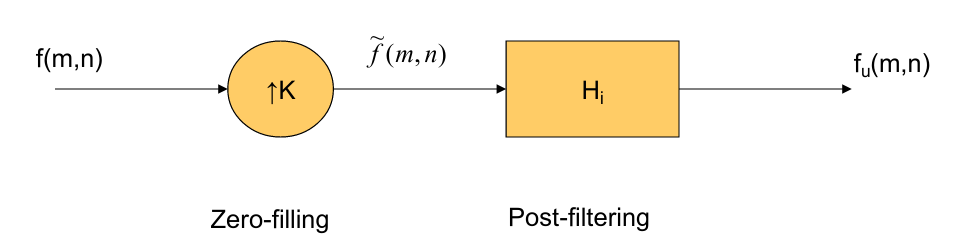 \(\begin{aligned} &\tilde{f}(m, n)=\left\{\begin{array}{cc} f(m / K, n / K) & \text { if } m, n \text { are multiple of } K \\ 0 & \text { otherwise } \end{array}\right. \\ &f_{u}(k, l)=\sum_{k, l} \tilde{f}(m, n) h(k-m, l-n)=\tilde{f}(k, l) * h(k, l) \end{aligned}\)
\(\begin{aligned} &\tilde{f}(m, n)=\left\{\begin{array}{cc} f(m / K, n / K) & \text { if } m, n \text { are multiple of } K \\ 0 & \text { otherwise } \end{array}\right. \\ &f_{u}(k, l)=\sum_{k, l} \tilde{f}(m, n) h(k-m, l-n)=\tilde{f}(k, l) * h(k, l) \end{aligned}\)
- nearest neighbor:新值取决于跟原图里哪个像素最近
- $\mathrm{O}\left[\mathrm{m}^{\prime}, \mathrm{n}^{\prime}\right]=\mathrm{I}[(\text { int })(\mathrm{m}+0.5),(\text { int })(\mathrm{n}+0.5)], \mathrm{m}=\mathrm{m}^{\prime} / \mathrm{M}, \mathrm{n}=\mathrm{n}^{\prime} / \mathrm{M}$
- bilinear 双线性内插值:新值用原图里最近的四个点线性加权平均
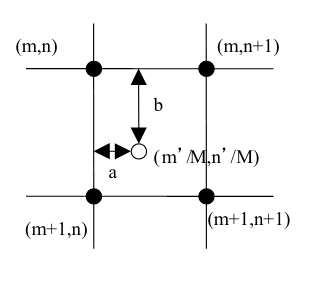
- 分开插值
- 比如先沿行算整行算新点的所在的列应该是多少 F[m,n’]=(1-a)I[m,n]+aI[m,n+1], a=n’-n.
- 之后再沿整列算新点所在的行应该是多少 O[m’,n’]=(1-b)F[m’,n]+bF[m’+1,n], b=m’-m
- 整体插值
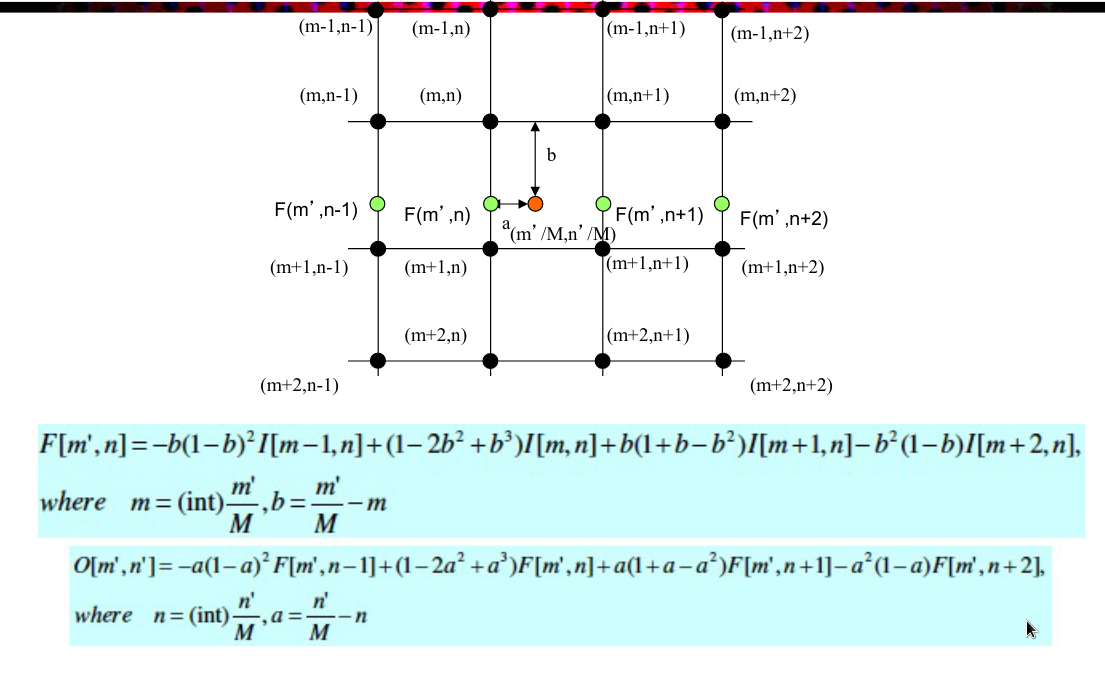
- 每个点的权重是新点和对角点组成矩形的面积 O[m’,n’]=(1-a)(1-b)I[m,n]+a(1-b)I[m,n+1]+(1-a)bI[m+1,n]+abI[m+1,n+1]
- 分开插值
- bicubic 双三次插值:新值用原图里最近16个点线性加权平均,系数里最高是a和b的立方 $$ \begin{aligned} F\left[m^{\prime}, n\right] &=-b(1-b)^{2} I[m-1, n]+\left(1-2 b^{2}+b^{3}\right) I[m, n]+b\left(1+b-b^{2}\right) I[m+1, n]-b^{2}(1-b) I[m+2, n] \quad m= (int) \frac{m^{\prime}}{M}, \quad b=\frac{m^{\prime}}{M}-m \
O\left[m^{\prime}, n^{\prime}\right]&=-a(1-a)^{2} F\left[m^{\prime}, n-1\right]+\left(1-2 a^{2}+a^{3}\right) F\left[m^{\prime}, n\right]+a\left(1+a-a^{2}\right) F\left[m^{\prime}, n+1\right]-a^{2}(1-a) F\left[m^{\prime}, n+2\right], where n= (int) \frac{n^{\prime}}{M}, a=\frac{n^{\prime}}{M}-n \end{aligned} $$
上采样周期变长,频率变小,可能会引入高频信号,上采样之后过一个half band filter 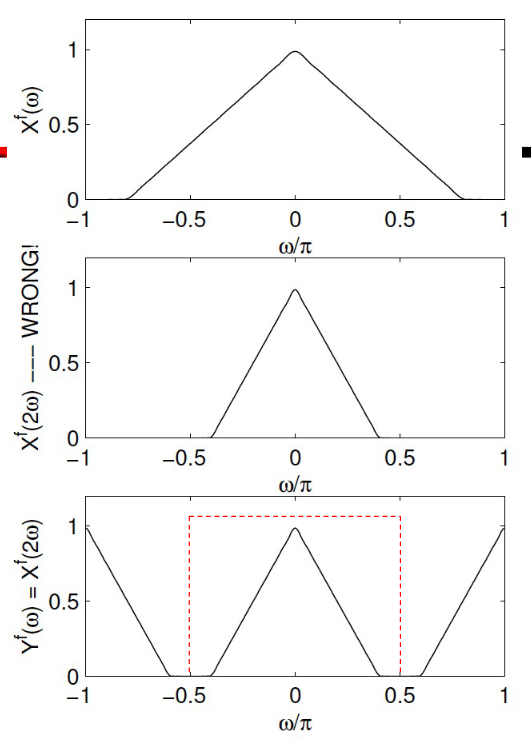
H hermission 转制+共扼
rou d
变换&压缩
N维空间里的所有向量都可以用N个线性无关的基底变换得来。
概念
- 内积:一个求共扼,和另一个对应位置相乘求和。几D都是,几D结果都是标量
- $A=(a_0, a_1, …, a_N),B=(b_0, b_1, …, b_N),A\cdot B=a_0b_0+a_1b_1+…+a_N*b_N$
- $A\cdot B=trace(AB^H)=trace(BA^H)$,trace是主对角线元素和,i,j相等的位置元素和
- 几何意义是投影
$A\cdot B= A B cos<A,B>$
- 外积 (TODO:)
- 单位正交基底:线性无关,都是单位长度,两两垂直
- 共轭转制:$X^H=(X^{*})^T$ hermitian
- 酉矩阵:单位正交列向量组成的矩阵,unitary matrix
- $酉矩阵^{-1}=酉矩阵^{H}$
- 酉矩阵U:$U^H U=U U^H=I$
符号
- N维
- $b_i$:一个基底,列向量
- B:$[b_0, b_1, …, b_{N-1}]$。基底列向量组成的N*N矩阵,必须可逆
- U:单位正交基底
- 通常排序从$b_0$到$b_{N-1}$ 频率越来越高
- U:单位正交基底
- S:信号列向量
- T:变换系数列向量,$S=B\cdot T$
- $E(\mathbf{X})$: 期望。$\mathbf{X}=(X_1, X_2, .., X_M)$, $E(\mathbf{X})$ 是 $\mathbf{X}$ 的期望,和 $\mathbf{X}$ 里的一个 $X$ 一样大
$Var(\mathbf{X})$:方差。$\sum {X-E(\mathbf{X})}\cdot{X-E(\mathbf{X})}^H$。每个$X$和所有$X$期望做差,这个差和自己的hermission乘,求和。结果和$X$一样大 \(b_i = \begin{bmatrix} b_{i,0} \\ b_{i,1} \\ .\\ .\\ .\\ b_{i,N-1} \\ \end{bmatrix}, B=[b_0, b_1, ... , b_{N-1}] \\ T = \begin{bmatrix} t_0 \\ t_1 \\ .\\ .\\ .\\ t_{N-1} \end{bmatrix} \\ S = \begin{bmatrix} s_0 \\ s_1 \\ .\\ .\\ .\\ s_{N-1} \end{bmatrix} \\\)
- 逆变:变换系数 $\rightarrow$ 信号,合成
- 信号在每个基底上的分量乘那个基底,横向做和 \(S=BT\)
- 正变:信号 $\rightarrow$ 变换系数,分解 \(T=B^{-1}S\)
- 对单位正交基底$U$,$U^{-1}=(U^*)^T$,记为$U^{H}$ \(T=U^{-1}S=U^{H}S\)
变换理解:在单位正交基底U上
- 正变:$T=U^HS$
- $U^H$中第k行是第k个基底$u_k$的共轭
- 矩阵相乘的时候,$U^H$第k行和信号对应位置相乘求和
- 就是 $u_k^*$ 和信号对应位置相乘求和
- 就是 $u_k\cdot S$
- 就是信号在 $u_k$ 上的投影
- 逆变:$S=UT$
- T中的第k个数是信号在第k个基底上的投影
- U的第k列是第k个基底
- UT可以看作U的第k列先乘T的第k个数,得到k个列矩阵之后再每行平均
一些变换
Hadmard \(\begin{aligned} &\mathbf{h}_{0}=\left[\begin{array}{l} 1 / 2 \\ 1 / 2 \\ 1 / 2 \\ 1 / 2 \end{array}\right], \mathbf{h}_{1}=\left[\begin{array}{c} 1 / 2 \\ 1 / 2 \\ -1 / 2 \\ -1 / 2 \end{array}\right], \mathbf{h}_{2}=\left[\begin{array}{c} 1 / 2 \\ -1 / 2 \\ -1 / 2 \\ 1 / 2 \end{array}\right], \mathbf{h}_{3}=\left[\begin{array}{c} 1 / 2 \\ -1 / 2 \\ 1 / 2 \\ -1 / 2 \end{array}\right] \\ &\mathbf{f}=\left[\begin{array}{l} 1 \\ 2 \\ 3 \\ 4 \end{array}\right] \Rightarrow\left\{\begin{array}{l} t_{0}=5 \\ t_{1}=-2 \\ t_{2}=0 \\ t_{3}=-1 \end{array}\right. \end{aligned}\)
离散傅立叶 DFT:第k个基底的频率是k圈,从一圈里采样N个点 \(\begin{aligned} &F(k)=\frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} f(n) e^{-j 2 \pi \frac{k n}{N}}, \quad k=0,1, \ldots, N-1 \\ &f(n)=\frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} F(k) e^{j 2 \pi \frac{k n}{N}}, \quad n=0,1, \ldots, N-1 \end{aligned}\)
- 离散余弦变换 DCT \(\begin{aligned} &h_{k}(n)=\alpha(k) \cos \left[\frac{(2 n+1) k \pi}{2 N}\right] \\ &\text { where } \alpha(k)= \begin{cases}\sqrt{1 / N} & k=0 \\ \sqrt{2 / N} & k=1, \ldots, N-1\end{cases} \end{aligned}\)
\(T(k)=\sum_{n=0}^{N-1} f(n) h_{k}(n) \\ f(n)=\sum_{u=0}^{N-1} T(k) h_{k}(n)\) (TODO:整理符号)
单位正交变换的统计性质
- $t_0=Avg(S)$
- 第一个基底$u_0$是单位长度,并且所有分量相等。$t_0$就是整个信号S的平均数
- $U^HE(\mathbf{S})=E(\mathbf{T}),UE(\mathbf{T})=E(\mathbf{S})$
- 多个信号经过正变得多个系数,信号们的均值 $E(\mathbf{S})$ 和系数们的均值 $E(\mathbf{T})$ 和一个基底都一样大
- 系数的期望就是样本的期望分解,样本的期望就是系数的期望合成
- $U^HVar(\mathbf{S})U=Var(\mathbf{T}),UVar(\mathbf{T})U^H=Var(\mathbf{S})$
- $X$ 是N维向量,$Var(\mathbf{X})$ 是N*N维向量,$Var(\mathbf{X})[i,j]$ 代表一堆 $X$,就是 $\mathbf{X}$ 中第i个维度和第j个维度的相关性
- 信号的方差先投影到各个基底上,得到信号的方差在各个基底上的系数,之后合成系数的方差;系数的方差先合成一个信号,得到每个系数对每个系数方差的信号,之后投影到各个基底上得到信号的方差
- 样本的方差就是系数的方差先合成再右乘$U^H$,系数的方差就是样本的方差先分解再右乘$U$
- 一组好的基底系数的方差应该尽可能对角 <!– - $Var(\mathbf{S})[i, j]$ 是信号第i维度和第j维度间的方差,这个矩阵的第j列是各个维度和第j个维度间的方差
- 定义 $P=U^HVar(S)$ ,P的第j列是 $Var(\mathbf{S})$ 中的第j列分别和每个基底做内积得来。所以P的第j列就是信号各个维度和第j个维度间的方差在各个基底上的投影
- P[a,j]是信号各个维度和第j个维度间的方差在第a个基底上的投影
- P中的第a行是信号各个维度和各个维度的方差在第a个基底上的投影
- 最后 PU[a,b] 是P的第a行和U的第b列对应位置相乘求和,是把信号的方差在第a个基底上的投影和第b个基底按位置相乘, –> (TODO:左乘和右乘的含义)
- 单位正交基底,信号平方和跟系数平方和相同;非单位正交基底,所有信号内的方差和所有系数内的方差和相同
- 平方是 $\sqrt{(x \times x^*)}$
- 丢掉一些高频分量,信号每个维度误差的平方和=丢掉的分量的系数平方和
比如对基底和信号 \(\begin{aligned} &\mathbf{h}_{0}=\left[\begin{array}{l} 1 / 2 \\ 1 / 2 \\ 1 / 2 \\ 1 / 2 \end{array}\right], \mathbf{h}_{1}=\left[\begin{array}{c} 1 / 2 \\ 1 / 2 \\ -1 / 2 \\ -1 / 2 \end{array}\right], \mathbf{h}_{2}=\left[\begin{array}{c} 1 / 2 \\ -1 / 2 \\ -1 / 2 \\ 1 / 2 \end{array}\right], \mathbf{h}_{3}=\left[\begin{array}{c} 1 / 2 \\ -1 / 2 \\ 1 / 2 \\ -1 / 2 \end{array}\right], \\ &\mathbf{f}=\left[\begin{array}{l} 1 \\ 2 \\ 3 \\ 4 \end{array}\right] \Rightarrow\left\{\begin{array}{l} t_{0}=5 \\ t_{1}=-2 \\ t_{2}=0 \\ t_{3}=-1 \end{array}\right. \end{aligned}\) 信号和系数的平方和都是30。只用$h_0$和$h_1$ \(\begin{gathered} \hat{f}=t_{0} h_{0}+t_{1} h_{1}=\frac{5}{2}\left[\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \end{array}\right]-\frac{2}{2}\left[\begin{array}{c} 1 \\ 1 \\ -1 \\ -1 \end{array}\right]=\frac{1}{2}\left[\begin{array}{l} 3 \\ 3 \\ 7 \\ 7 \end{array}\right], \mathrm{e}=f-\hat{f}=\frac{1}{2}\left[\begin{array}{l} 2 \\ 4 \\ 6 \\ 8 \end{array}\right]-\frac{1}{2}\left[\begin{array}{l} 3 \\ 3 \\ 7 \\ 7 \end{array}\right]=\frac{1}{2}\left[\begin{array}{c} -1 \\ 1 \\ -1 \\ 1 \end{array}\right] \\ ||e||^2=1, t_{2}^{2}+t_{3}^{2}=1 \end{gathered}\) e的平方和跟没用的两个系数的平方和都是1
- 2D可分离基底:一套2D基底由一套1D基底矩阵相乘$h_ah_b^T$或者向量外积得来
- 不是单个基底是可分矩阵,是用一套1D基底$h_ah_b^T$生成一套2D基底
- 2D单位正交基底:和自己内积和都是1,和别人内积和都是0
2D DCT基底
2D hadamard 基底:只有0,1,没有DCT细,但是只需要做加法
计算量
- 不可分:$N^4$
- $N^2$个基底,每个基底内积$N^2$次乘法
- 可分:$2N^3$
- 每行做1D变换,得到N个中间结果。一行$N$次乘法,每个图$N^2$,一共N个1D基底,总共$N^3$次乘法
- 对每个中间结果每列做1D变换,得到$N^2$个最终结果。也是$N^3$次乘法
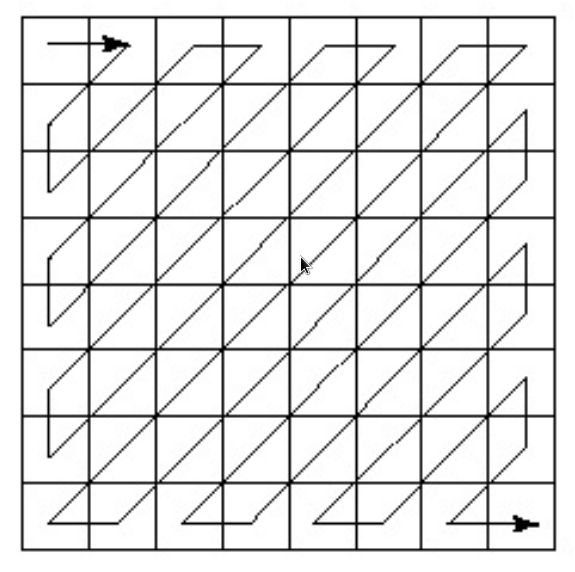
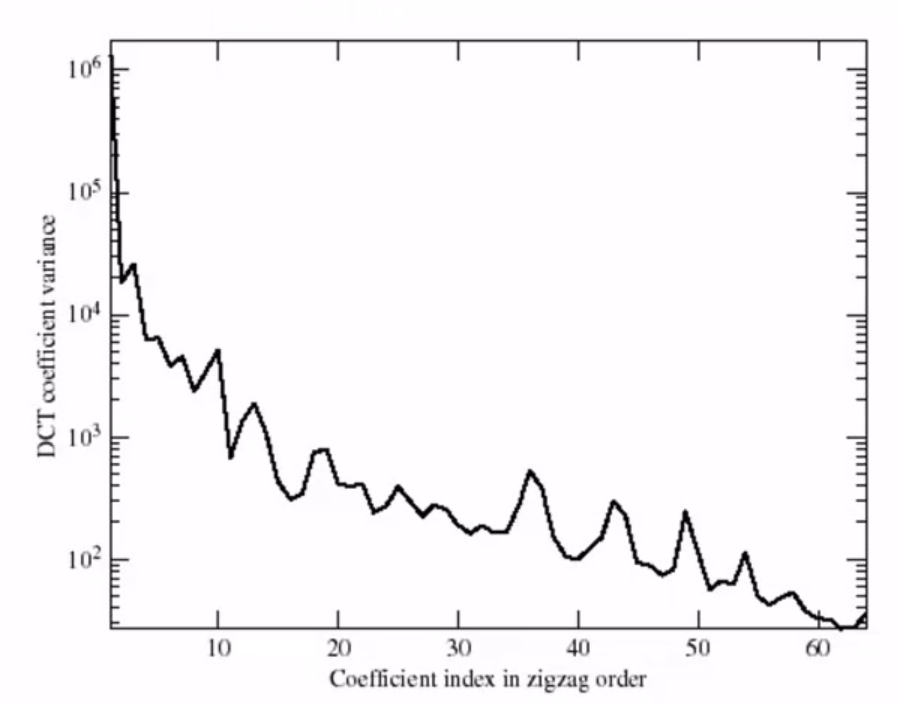
按照zig-zag顺序频率变高,低频信号的方差大,变化更多。只保留低频分量重建误差小
扔掉了高频分量,斜线变得台阶
最好的变换基底
好的变换基底
- 系数相关性小
- 能量集中:系数里少量大的,其他都接近0
- 计算简单:2D会选比较小的维度,否则计算量很大
- 2D可分离
用于
- 压缩
- 降低特征维度
- 降噪
KLT变换
信号相关,基底是信号协方差矩阵的正交特征矢量。系数就是特征值
PCA
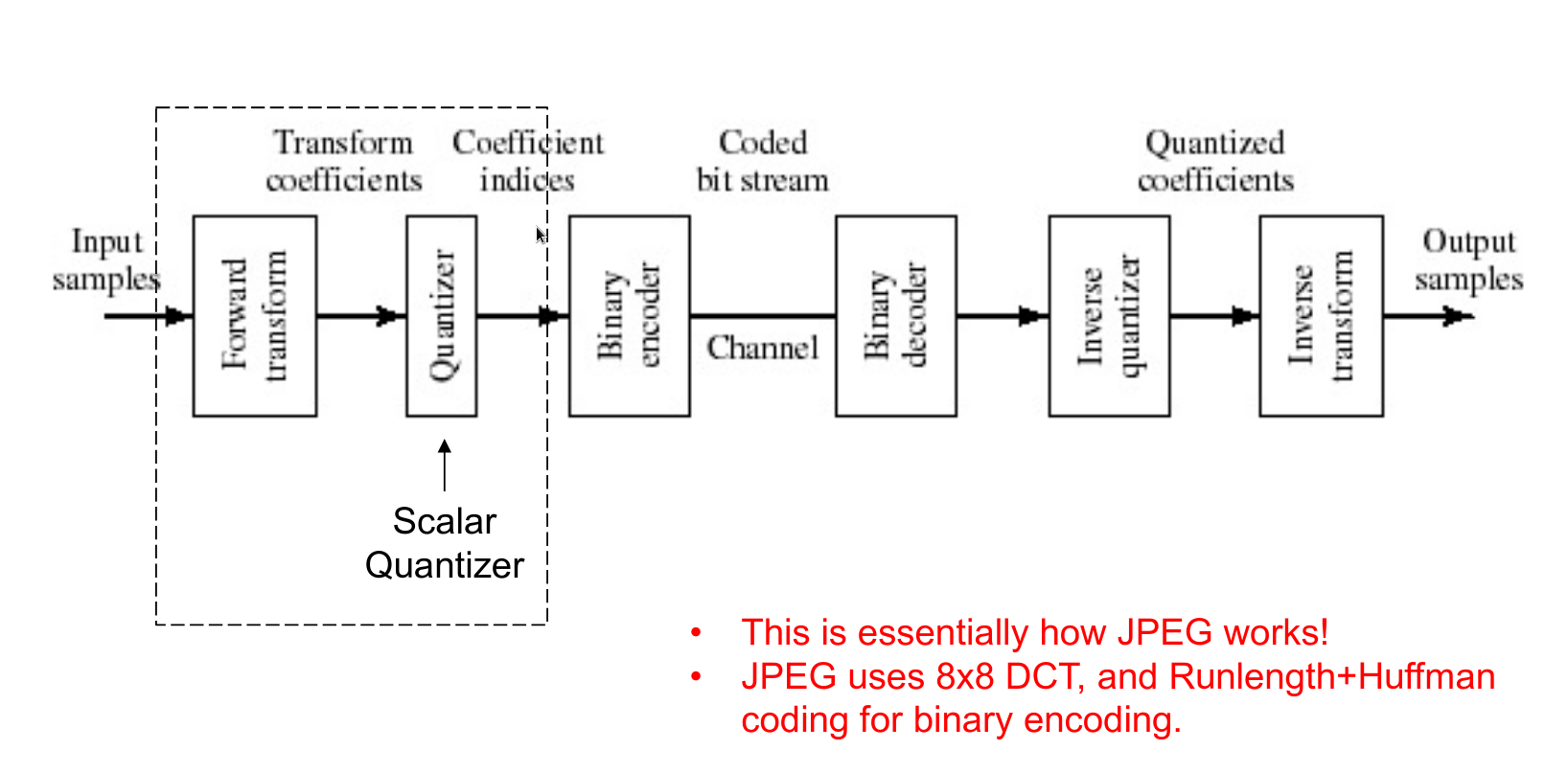
变换编码流程
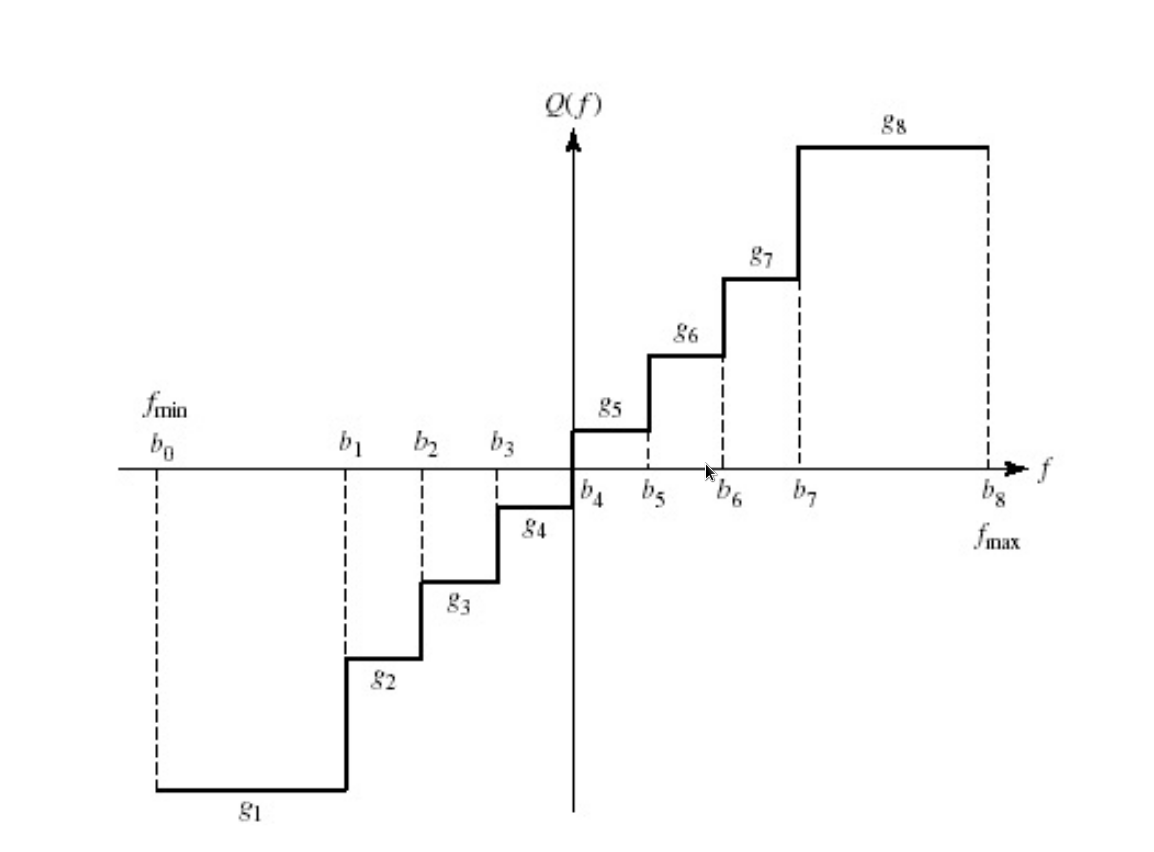
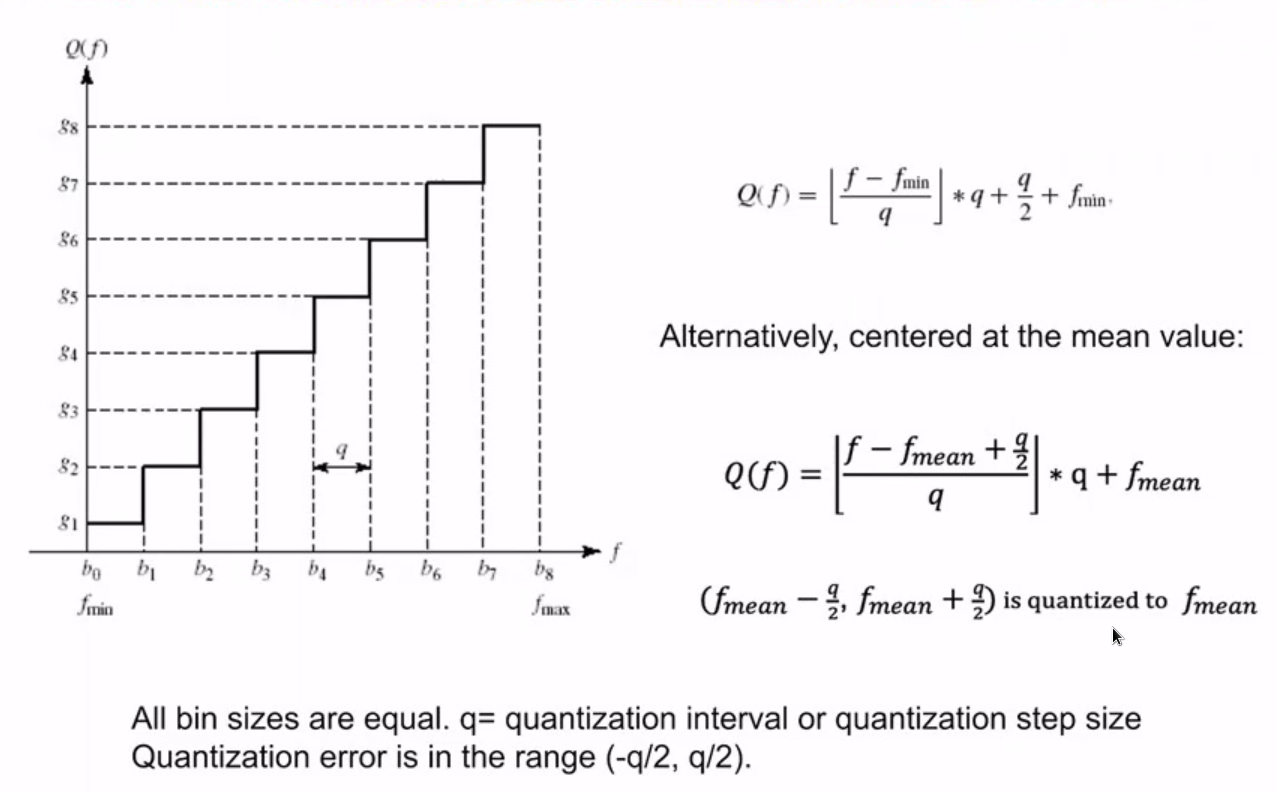
量化
编码
- 定长
- 变长:出现的越多,编码越短
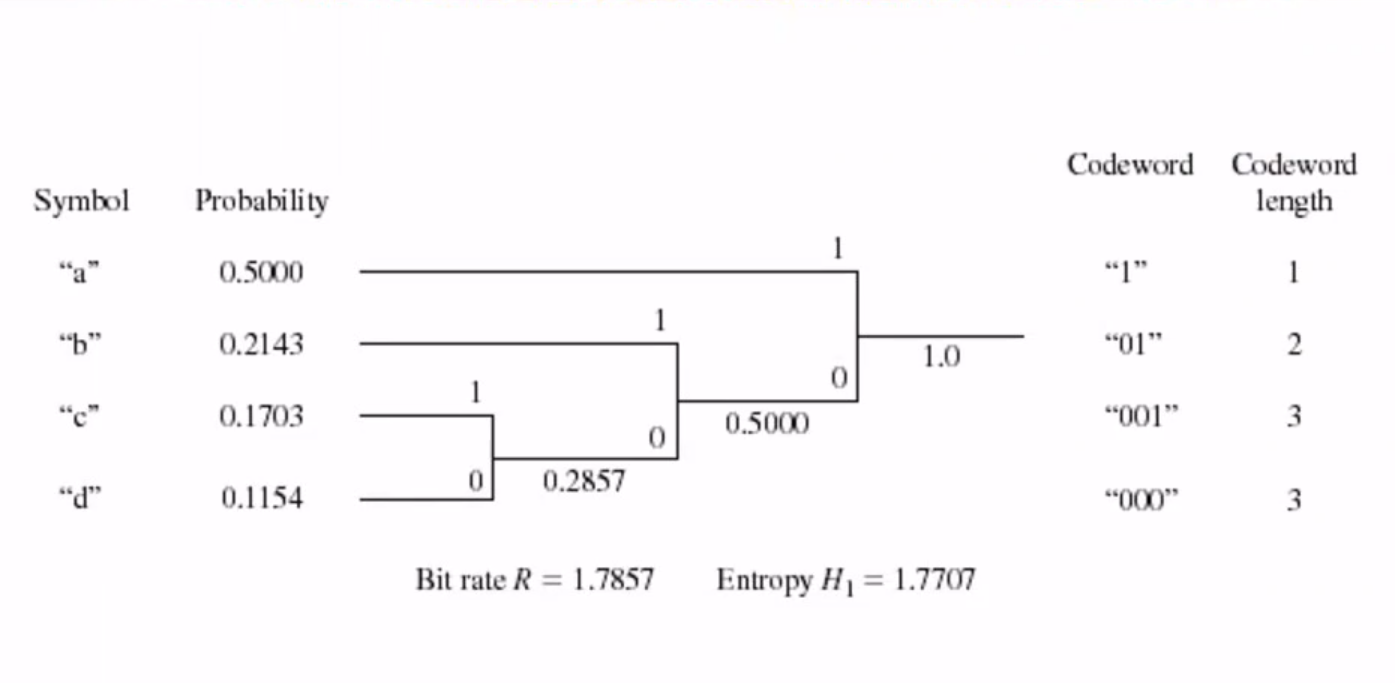
比特率:每个情况的概率编码这个情况的bit数 信息熵:$H(f)=-\sum_k p(k)log_2p(k)$,每个概率$log_2(概率)$的和的相反数。信息熵是编码这个概率分布最少需要的bit数
K=2
- 概率[1,0], [0,1]的信息熵是0
- 概率分布越平均,信息熵越大,[0.5, 0.5]最大,信息熵是1
从概率最低的两个开始,合并成一个情况,合并后的概率是这两个的和,一个给1,一个给0。反复,页节点给1,子树给0。
有时候两个情况经常固定顺序出现,这样编码连续的两个值,$K^2$种情况可能比编码K种情况比特率低
JPEG
JPEG
- 所有值-128
- 8*8 DCT
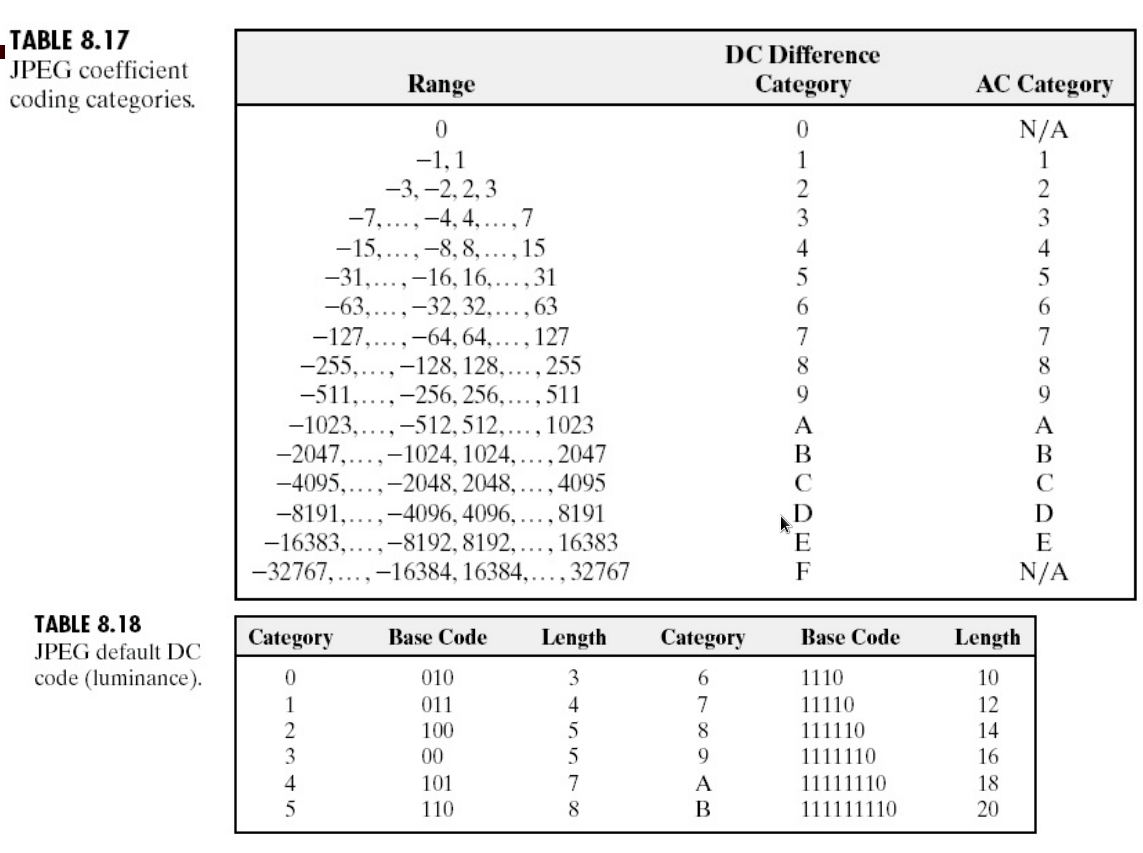
- DC信号
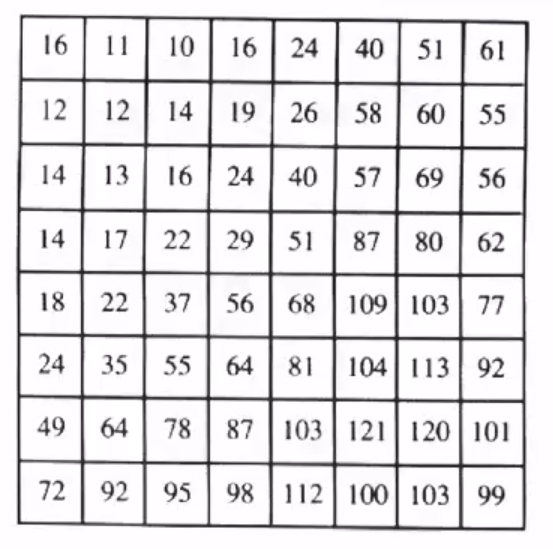
- 量化
- 行程长度压缩,每个非0值存(和前一个非0值之间多少个0,具体值)
- 在所有行程长度对上进行编码
- huffman:有默认huffman编码表,也可以在图片里带
- 算数编码:压缩率高,计算复杂
- 除了整体出现频率以外,空间位置上的条件概率也是信息,跟DC一样先推测再记录错误
- 黑白图
- 彩色
- JPEG-LS:无损压缩或基本无损
- JPEG2000:波长变换,无损
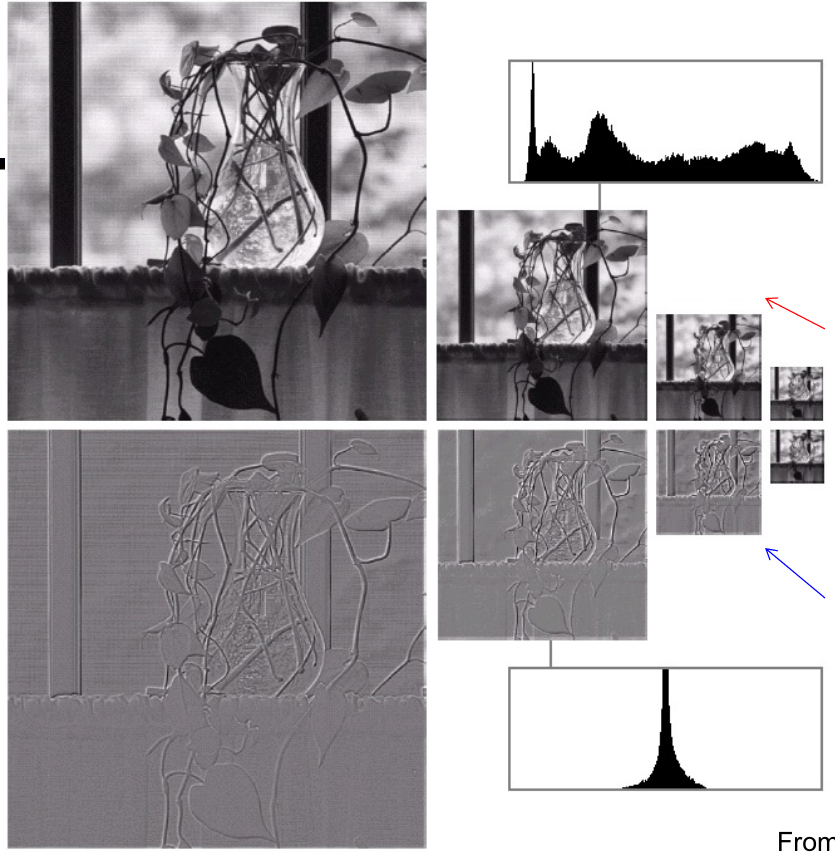
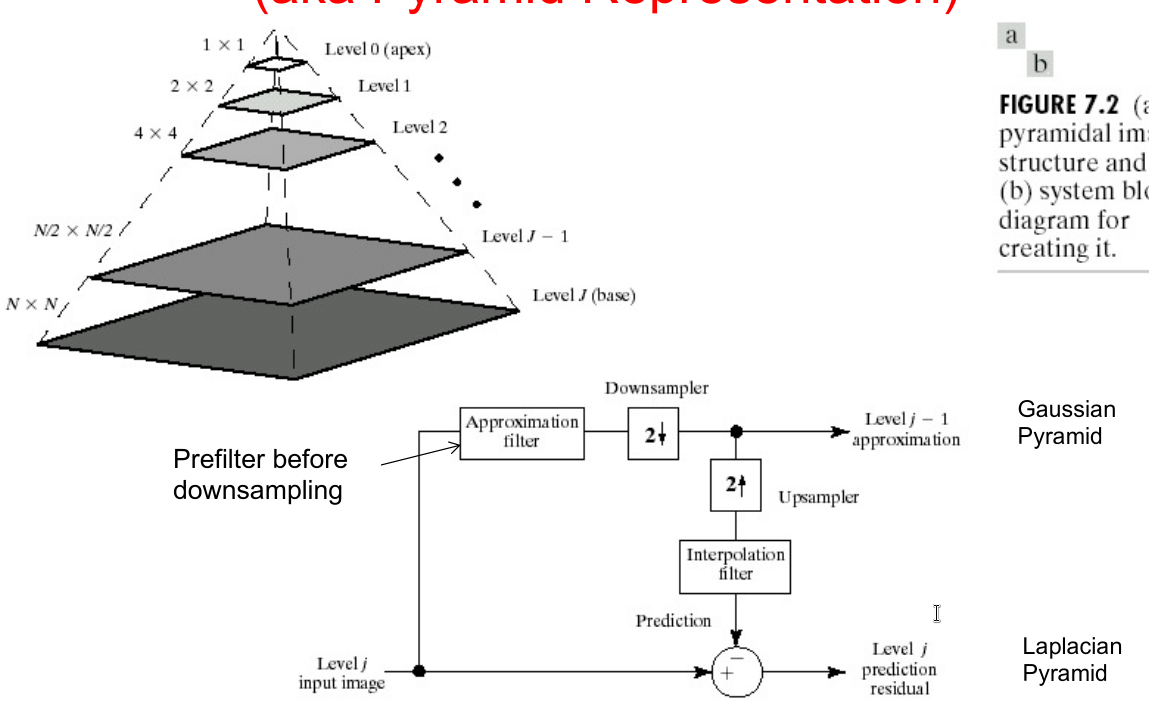
金字塔
- 冗余表示,增加 $\frac{1}{3}N^2$ 数据量
- 不断下采样
- 采样结果是高斯
- 用下采样结果推测原尺度,推测和原尺度的參差是拉普拉斯
- 上:高斯金字塔
- 下:拉普拉斯金字塔,接近0的值很多
用途
- SIFT:抽取不同大小的同一特征
- 多尺度特征提取和检测
- 在高层抽象上计算更快
- 降噪:去掉高层(大图)拉普拉斯图像高频特征
- 压缩
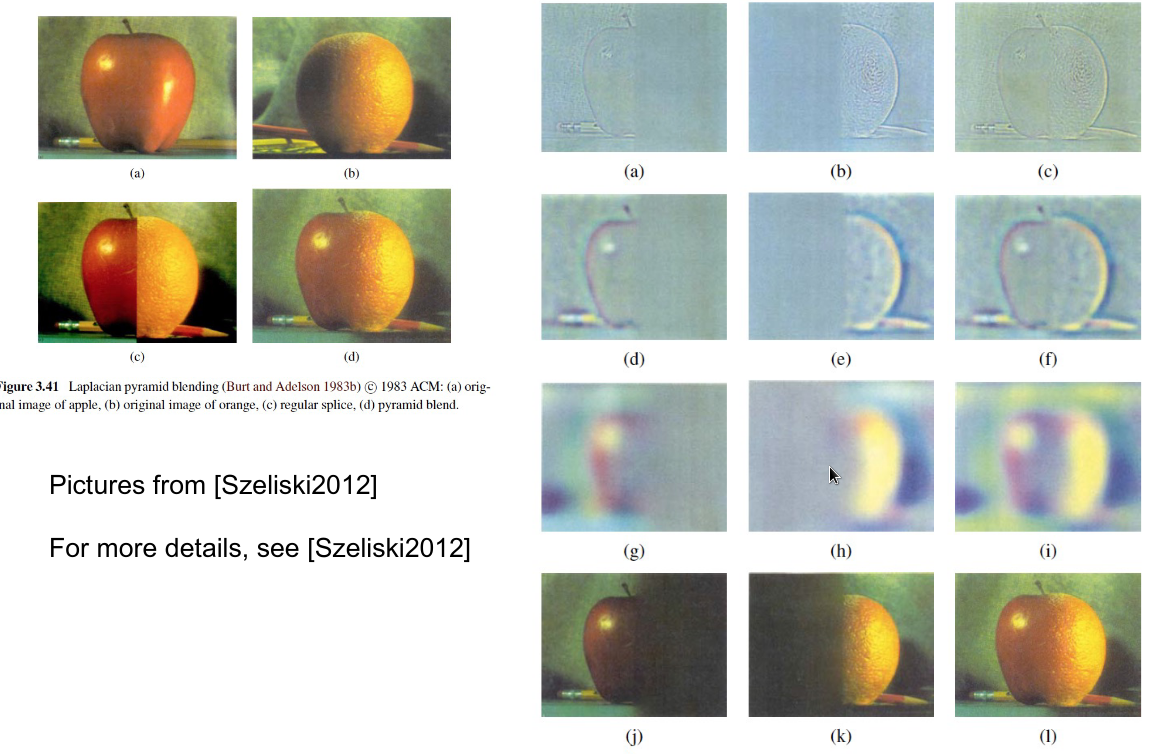
- 更自然的图像融合
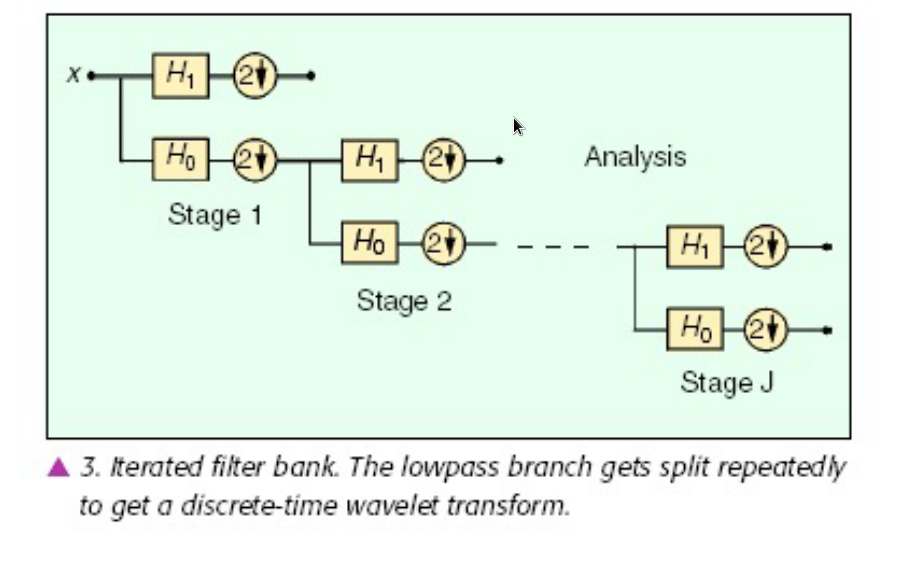
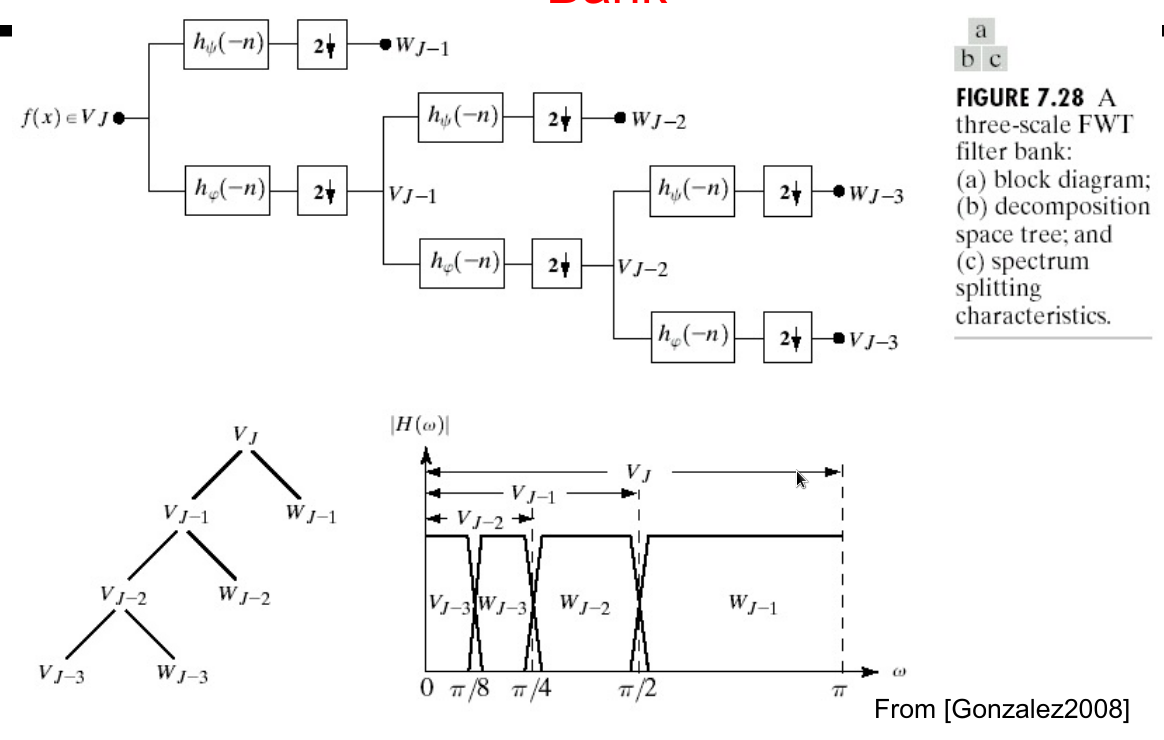
小波分析
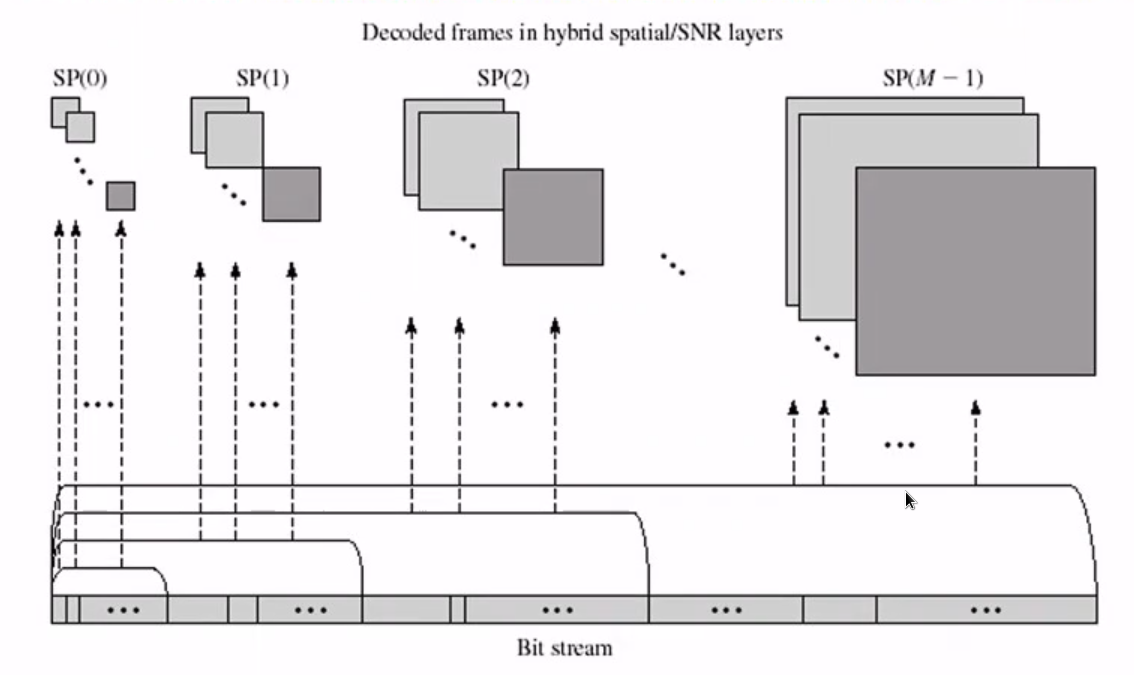
- 不冗余
- 方便重建小图:收到一个尺度就可以重建到一个尺度
- 在整个图像上进行变换,没有块状伪影
$h 0$ : averaging, $[1,1] / \sqrt{2} ; \quad h 1$ : difference, $[1,-1] / \sqrt{2}$; \(g 0=[1,1] / \sqrt{2} ; \quad g 1=[-1,1] / \sqrt{2}\)
- 低频:平均
- 高频:做差
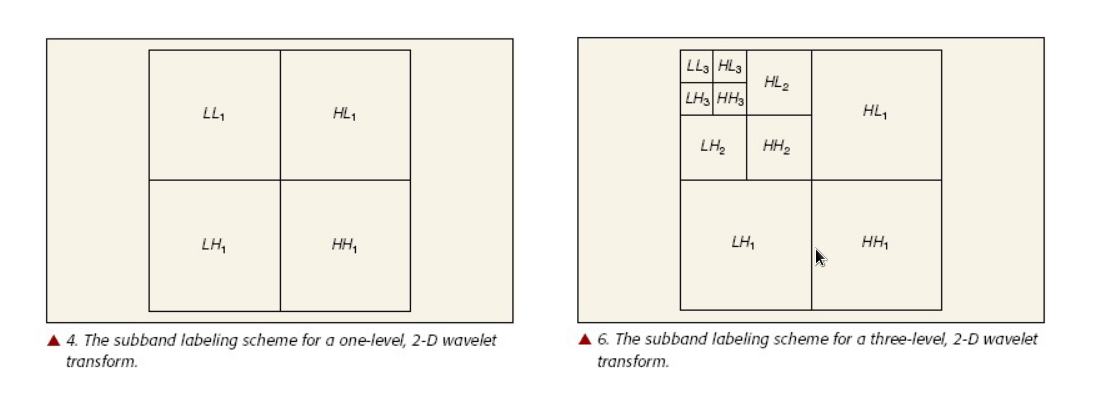
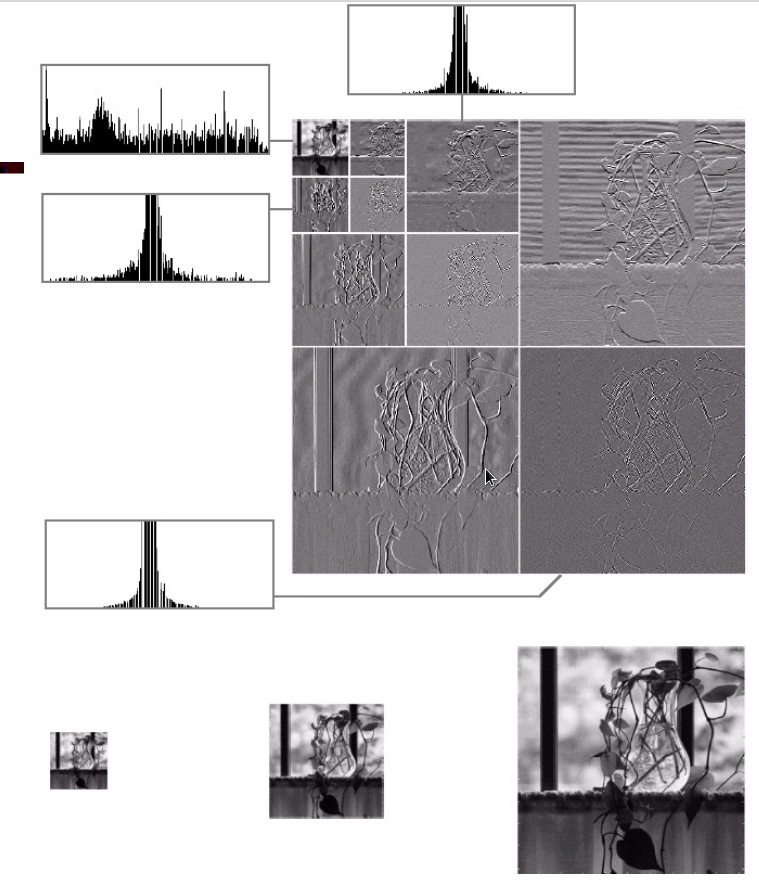
 行列分别进行,一个阶段包含一次行一次列,出四张图。多阶段继续分析LL
行列分别进行,一个阶段包含一次行一次列,出四张图。多阶段继续分析LL
降噪